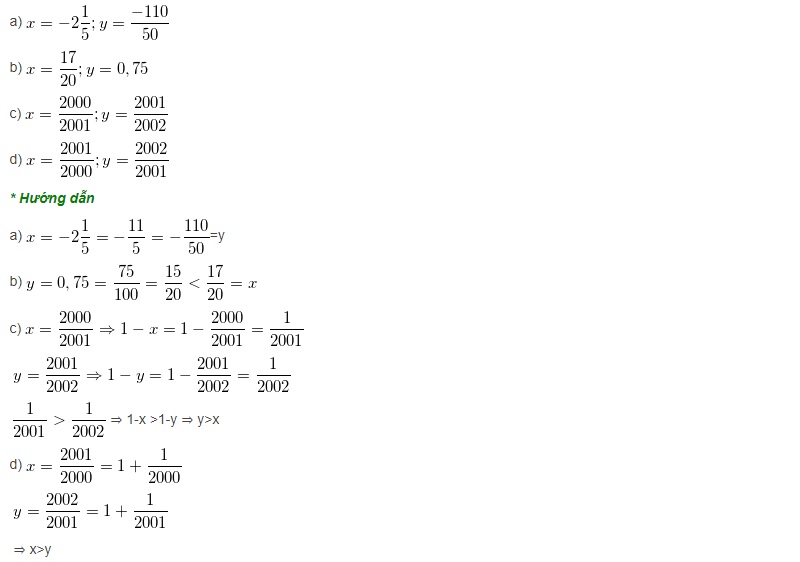Trong toán học, số hữu tỉ là một khái niệm cơ bản và rất quen thuộc. Các số hữu tỉ được định nghĩa là các số có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b khác 0. Tập hợp các số hữu tỉ được ký hiệu là Q. Trong bài viết này, chúng ta sẽ cùng tìm hiểu sâu hơn về số hữu tỉ, phân loại và các phép toán liên quan đến chúng.

Đặc điểm của số hữu tỉ
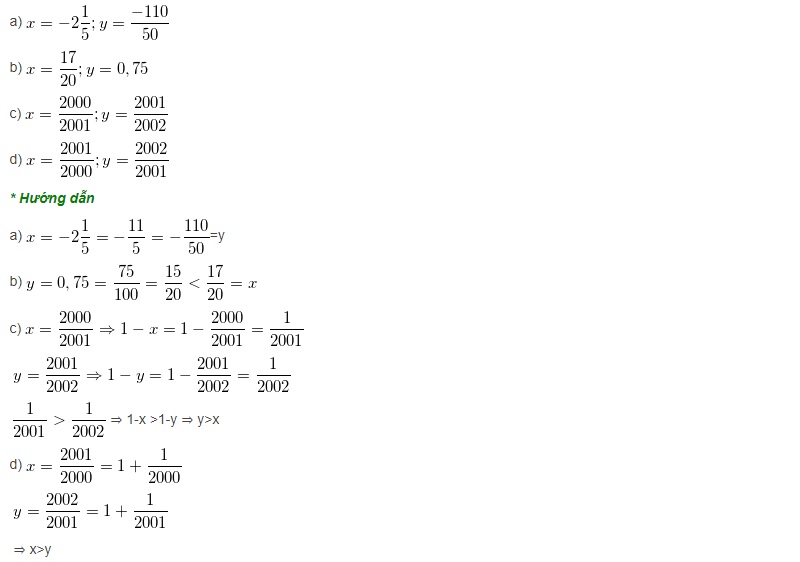
1. Định nghĩa
Số hữu tỉ được định nghĩa như sau:
- Số hữu tỉ là các số có thể viết dưới dạng a/b, với a, b ∈ Z (b là số nguyên và b ≠ 0).

2. Ví dụ về số hữu tỉ
Một số ví dụ điển hình về số hữu tỉ bao gồm:
- 3 (có thể viết dưới dạng 3/1)
- -1/2 (số âm)
- 2/3
Các số thuộc tập hợp số hữu tỉ Q có thể bao gồm cả số thập phân hữu hạn, số thập phân vô hạn tuần hoàn và các số nguyên.

3. Phân loại các số hữu tỉ
Tập hợp Q bao gồm các loại số sau:
- Số thập phân hữu hạn: Ví dụ: 0.5 (½), 0.2 (⅕)
- Số thập phân vô hạn tuần hoàn: Ví dụ: 0.16666… (⅙), 0.3333… (⅓)
- Số nguyên (Z): Ví dụ: -2, -1, 0, 1, 2
- Số tự nhiên (N): Ví dụ: 1, 2, 3, 4, 5, 6

Tính chất của số hữu tỉ
- Tập hợp số hữu tỉ Q là một tập hợp đếm được.
- Các phép toán cộng và trừ với số hữu tỉ được thực hiện dễ dàng bằng cách quy đồng mẫu số.
- Nếu một số hữu tỉ là số hữu tỉ dương, thì số đối của nó là số hữu tỉ âm và ngược lại. Tổng của số hữu tỉ và số đối của nó bằng 0.

Tập hợp số hữu tỉ Q

Phân loại
Tập hợp Q có thể được phân chia thành hai loại chính:
- Số hữu tỉ dương: Các số lớn hơn 0.
- Số hữu tỉ âm: Các số nhỏ hơn 0.
Lưu ý rằng số 0 không thuộc vào cả hai loại trên.
Các phép toán cơ bản với số hữu tỉ
1. Phép tính cộng và trừ
Để thực hiện phép tính cộng và trừ với số hữu tỉ, bạn có thể làm theo các bước sau:
- Bước 1: Viết các số hữu tỉ dưới dạng phân số.
- Bước 2: Áp dụng quy tắc cộng và trừ, đưa các số về cùng mẫu, rồi cộng hoặc trừ tử số.
- Bước 3: Rút gọn kết quả (nếu có thể).
2. Phép tính nhân và chia
- Nhân hai số hữu tỉ: Nhân hai tử số với nhau và hai mẫu số với nhau.
- Chia hai số hữu tỉ: Nhân số thứ nhất với mẫu số của số thứ hai và mẫu số của số thứ nhất với tử số của số thứ hai.
3. Giá trị tuyệt đối của số hữu tỉ
Giá trị tuyệt đối của số hữu tỉ x, ký hiệu là |x|, là khoảng cách từ điểm x đến điểm O trên trục số. Công thức tính giá trị tuyệt đối như sau:
- Nếu x > 0 thì |x| = x.
- Nếu x = 0 thì |x| = 0.
- Nếu x < 0 thì |x| = -x.
4. So sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ x và y, bạn có thể thực hiện các bước sau:
- Viết x và y dưới dạng phân số cùng mẫu dương.
- So sánh các tử số a và b.
- Nếu a > b thì x > y.
- Nếu a = b thì x = y.
- Nếu a < b thì x < y.
Số vô tỉ là gì?
1. Định nghĩa
Số vô tỉ là tất cả các số thực không phải là số hữu tỉ, tức là các số không thể biểu diễn dưới dạng tỉ số của các số nguyên. Số vô tỉ thường được viết dưới dạng số thập phân vô hạn không tuần hoàn.
2. Ví dụ về số vô tỉ
- Số vô tỉ: 0,1010010001000010000010000001… (số thập phân vô hạn không tuần hoàn)
- Số căn bậc 2: √2
- Số pi (π): 3.14159…
3. Tính chất của số vô tỉ
Tập hợp số vô tỉ là một tập hợp không đếm được, có nghĩa là không thể liệt kê hết các số vô tỉ.
Sự khác nhau giữa số hữu tỉ và số vô tỉ
- Số hữu tỉ bao gồm số thập phân vô hạn tuần hoàn.
- Số vô tỉ là số thập phân vô hạn không tuần hoàn.
- Số hữu tỉ chỉ là phân số.
- Số vô tỉ bao gồm rất nhiều loại số khác nhau.
- Số hữu tỉ là số đếm được.
- Số vô tỉ là số không đếm được.
Các dạng bài tập về tập hợp Q - số hữu tỉ và phương pháp giải
Dạng 1: Thực hiện phép tính với số hữu tỉ
Phương pháp giải: Đầu tiên, viết 2 số hữu tỉ đã cho dưới dạng phân số, rồi áp dụng quy tắc tính toán để tính và đưa ra đáp số chính xác.
Dạng 2: Biểu diễn tập hợp Q trên trục số
Phương pháp giải:
- Nếu a/b là số hữu tỉ dương, chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau.
- Nếu a/b là số hữu tỉ âm, thực hiện tương tự nhưng trong chiều âm của trục số.
Dạng 3: So sánh các số hữu tỉ
Phương pháp giải: Đưa các số hữu tỉ đã cho dưới dạng phân số có cùng mẫu số dương rồi so sánh tử số.
Dạng 4: Tìm điều kiện để một số hữu tỉ là âm, dương hoặc là 0
Phương pháp giải: Dựa vào tính chất của số hữu tỉ để xác định đó là số âm, dương hay là 0.
Dạng 5: Tìm các số hữu tỉ nằm trong một khoảng
Phương pháp giải: Đưa các số hữu tỉ đó về cùng mẫu hoặc tử số.
Dạng 6: Tìm x để biểu thức nguyên
Phương pháp giải: Quy đồng khử mẫu số, rồi chuyển các số hạng chứa x về một vế, các số hạng còn lại về một vế.
Dạng 7: Các bài toán tìm x với số hữu tỉ
Phương pháp giải: Quy đồng khử mẫu số rồi tiến hành tìm x.
Dạng 8: Bài toán tìm x trong các bất phương trình
Phương pháp giải: Tương tự như các dạng trên, căn cứ vào tính chất số hữu tỉ.
Dạng 9: Tính tổng tập hợp Q là các số hữu tỉ theo quy tắc
Phương pháp giải: Sử dụng quy tắc tính tổng cho các số hạng cách nhau một số không đổi hoặc gấp n lần số đứng trước.
Một số bài tập mẫu về tập hợp Q - số hữu tỉ tự luyện
Để củng cố kiến thức, các bạn có thể tham khảo và thực hành với các bài tập mẫu về số hữu tỉ. Việc làm nhiều bài tập sẽ giúp bạn nắm vững các khái niệm và phương pháp giải.
Hy vọng, thông qua những chia sẻ trên về số hữu tỉ và số vô tỉ, bạn sẽ có cái nhìn rõ ràng hơn về khái niệm và ứng dụng của chúng trong toán học. Hãy cùng nhau khám phá và học hỏi thêm nhiều điều thú vị về toán học nhé!