Viện Đào Tạo Vinacontrol luôn cập nhật và cung cấp những kiến thức chuẩn xác, hữu ích trong lĩnh vực kiểm định, đo lường và quản lý chất lượng. Một trong những khái niệm quan trọng trong hình học không gian mà chúng ta không thể bỏ qua là diện tích xung quanh của hình nón. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán một cách hiệu quả mà còn hỗ trợ trong việc kiểm tra tiêu chuẩn kỹ thuật của nhiều công trình và thiết bị.

1. Hình Nón Là Gì?
Hình nón là một khối hình học không gian có đáy là một hình tròn và đỉnh là một điểm duy nhất không nằm trong mặt phẳng đáy. Đối với hình nón, hai yếu tố quan trọng nhất chính là đáy và đỉnh, chúng tạo nên các đường sinh, giúp hình nón có dạng hình trụ thon gọn, kéo dài từ đỉnh xuống chu vi của đáy.
Hình nón được ứng dụng rộng rãi trong thực tế, từ thiết kế tháp, ống khói cho đến các cấu trúc yêu cầu độ chắc chắn nhưng vẫn đảm bảo tính thẩm mỹ và sự nhẹ nhàng.

2. Công Thức Tính Diện Tích Xung Quanh Hình Nón
2.1 Định Nghĩa Diện Tích Xung Quanh
Diện tích xung quanh của hình nón là phần diện tích bao quanh hình nón, không bao gồm diện tích của đáy. Để tính diện tích xung quanh, chúng ta cần sự hỗ trợ từ bán kính của đáy và chiều dài của đường sinh.
2.2 Công Thức Tính Diện Tích Xung Quanh
Công thức tính diện tích xung quanh hình nón được thể hiện như sau:
Sxq = πrl
Trong đó:
- Sxq là diện tích xung quanh.
- r là bán kính của đáy.
- l là độ dài của đường sinh.
- π (pi) ≈ 3.1416.
2.3 Ví Dụ Minh Họa
Giả sử bạn có một hình nón với bán kính đáy là 6 cm và độ dài đường sinh là 10 cm. Áp dụng công thức trên:
Sxq = π × 6 × 10 = 188.5 cm²
Vậy diện tích xung quanh của hình nón là 188.5 cm².
3. Các Công Thức Liên Quan Đến Hình Nón
Khi nghiên cứu về hình nón, không chỉ có công thức tính diện tích xung quanh mà còn có nhiều công thức quan trọng khác, như tính đường sinh, diện tích đáy, diện tích toàn phần, và thể tích của hình nón.
3.1 Công Thức Tính Đường Sinh
Đường sinh của hình nón là đoạn thẳng nối từ đỉnh hình nón đến một điểm trên đường tròn đáy. Để tính được đường sinh l, ta sử dụng định lý Pythagore với chiều cao h và bán kính đáy r:
l = √(h² + r²)
Trong đó:
- l là độ dài đường sinh.
- h là chiều cao của hình nón, tính từ đỉnh đến trung điểm của đáy.
- r là bán kính của đáy hình tròn, tức là khoảng cách từ tâm đến mép của đáy hình nón.
3.2 Công Thức Tính Diện Tích Đáy & Toàn Phần Hình Nón
Diện tích đáy của hình nón được tính theo công thức diện tích hình tròn:
Sđ = πr²
Diện tích toàn phần của hình nón bao gồm diện tích xung quanh và diện tích của đáy:
Stp = Sxq + Sđ = πrl + πr² = πr(l + r)
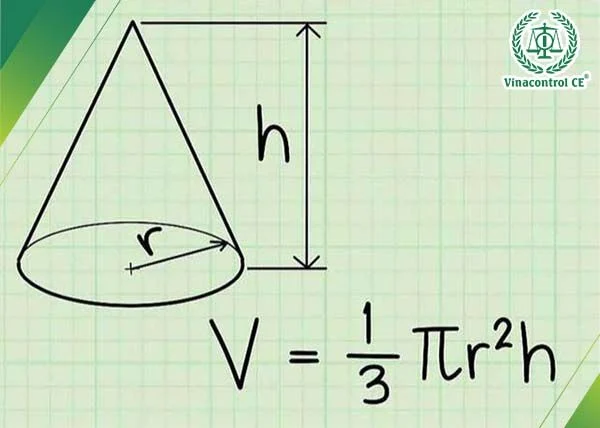
3.3 Công Thức Tính Thể Tích Của Hình Nón
Thể tích của hình nón được tính bằng cách sử dụng chiều cao và diện tích đáy, theo công thức:
V = (1/3)πr²h
Trong đó:
- V là thể tích.
- r là bán kính đáy.
- h là chiều cao của hình nón.
4. Bài Tập Vận Dụng và Lời Giải Chi Tiết
4.1 Dạng Bài Tập Cơ Bản
Bài Tập 1: Tính Diện Tích Xung Quanh Của Hình Nón
Đề bài: Cho hình nón có bán kính đáy r = 6 cm và độ dài đường sinh l = 10 cm. Tính diện tích xung quanh của hình nón.
Giải: Áp dụng công thức tính diện tích xung quanh hình nón:
Sxq = πrl = 3.1416 × 6 × 10 = 188.5 cm²
Vậy, diện tích xung quanh của hình nón là
188.5 cm².
Bài Tập 2: Tính Diện Tích Toàn Phần Của Hình Nón
Đề bài: Một hình nón có bán kính đáy r = 5 cm và độ dài đường sinh l = 13 cm. Tính diện tích toàn phần của hình nón.
Giải:
- Diện tích xung quanh: Sxq = πrl = 3.1416 × 5 × 13 = 204.2 cm²
- Diện tích đáy: Sđ = πr² = 3.1416 × 5² = 78.54 cm²
- Diện tích toàn phần: Stp = Sxq + Sđ = 204.2 + 78.54 = 282.74 cm²
Vậy, diện tích toàn phần của hình nón là
282.74 cm².
Bài Tập 3: Tính Thể Tích Của Hình Nón
Đề bài: Cho hình nón có bán kính đáy r = 7 cm và chiều cao h = 9 cm. Tính thể tích của hình nón.
Giải: Áp dụng công thức tính thể tích hình nón:
V = (1/3)πr²h = (1/3) × 3.1416 × 7² × 9 = 461.81 cm³
Vậy, thể tích của hình nón là
461.81 cm³.
4.2 Dạng Bài Tập Nâng Cao
Bài Tập 1: Tính Diện Tích Toàn Phần Hình Nón Có Điều Kiện Đặc Biệt
Đề bài: Cho hình nón có đường kính đáy d = 12 cm, chiều cao h = 8 cm. Tính diện tích toàn phần của hình nón.
Giải:
- Tính bán kính: r = d/2 = 6 cm
- Tính đường sinh: l = √(h² + r²) = √(8² + 6²) = √(64 + 36) = √100 = 10 cm
- Diện tích xung quanh: Sxq = πrl = 3.1416 × 6 × 10 = 188.5 cm²
- Diện tích đáy: Sđ = πr² = 3.1416 × 6² = 113.1 cm²
- Diện tích toàn phần: Stp = Sxq + Sđ = 188.5 + 113.1 = 301.6 cm²
Vậy, diện tích toàn phần của hình nón là
301.6 cm².
Bài Tập 2: Tính Diện Tích Xung Quanh Của Hình Nón Cụt
Đề bài: Cho hình nón cụt có bán kính đáy lớn r1 = 10 cm, bán kính đáy nhỏ r2 = 6 cm và độ dài đường sinh l = 15 cm. Tính diện tích xung quanh của hình nón cụt.
Giải: Áp dụng công thức tính diện tích xung quanh của hình nón cụt:
Sxq = π(r1 + r2)l = 3.1416 × (10 + 6) × 15 = 753.98 cm²
Vậy, diện tích xung quanh của hình nón cụt là
753.98 cm².
Bài Tập 3: Tính Thể Tích Của Hình Nón Khi Biết Góc Ở Đỉnh
Đề bài: Cho một hình nón có góc ở đỉnh 60°, bán kính đáy r = 10 cm. Tính thể tích hình nón biết rằng chiều cao bằng nửa độ dài đường sinh.
Giải:
- Chiều cao bằng nửa đường sinh: h = l/2
- Tính đường sinh: l = r/sin(30°) = 10/0.5 = 20 cm
- Tính chiều cao: h = 20/2 = 10 cm
- Tính thể tích: V = (1/3)πr²h = (1/3) × 3.1416 × 10² × 10 = 1047.2 cm³
Vậy, thể tích của hình nón là
1047.2 cm³.
5. Lưu Ý Khi Giải Các Bài Toán Về Hình Nón
- Nắm vững các công thức cơ bản và biết cách áp dụng chúng vào bài toán cụ thể.
- Khi tính toán liên quan đến đường sinh, cần cẩn thận áp dụng đúng định lý Pythagore để tính toán chính xác.
- Các bài tập nâng cao thường đòi hỏi kỹ năng giải toán kết hợp giữa nhiều công thức hoặc điều kiện đặc biệt, vì vậy cần đọc kỹ đề bài để tìm ra cách giải hợp lý.
Những bài tập cơ bản và nâng cao về hình nón sẽ giúp bạn rèn luyện và hiểu sâu hơn về cách tính toán liên quan đến hình học không gian.
Thông qua các bài tập và kiến thức chi tiết, hy vọng bạn đã có cái nhìn rõ hơn về cách áp dụng các công thức vào thực tiễn và nắm vững kiến thức cơ bản về hình nón, đặc biệt là diện tích xung quanh của hình nón.
Xem thêm:
- Công thức tính diện tích hình vuông và Bài tập có lời giải.
- Công thức tính diện tích hình bình hành và Hướng dẫn giải bài tập chi tiết.
- Công thức tính diện tích hình chữ nhật và các dạng bài tập hay có trong đề thi.
- Các công thức tính diện tích hình tam giác.
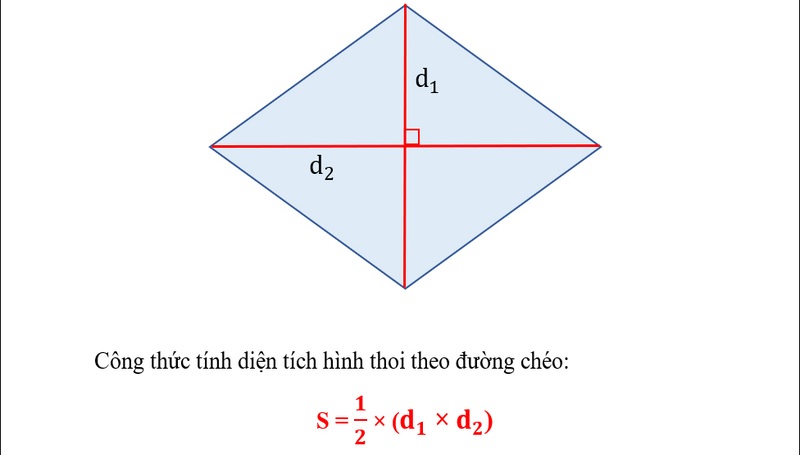
- Công thức tính diện tích hình thoi và cách giải bài tập chi tiết.
Hãy theo dõi các bài viết tiếp theo từ Viện Đào Tạo Vinacontrol để cập nhật thêm nhiều kiến thức thú vị và bổ ích!