Hình học là một trong những lĩnh vực quan trọng nhất trong chương trình giáo dục, đặc biệt ở bậc Trung học cơ sở và Trung học phổ thông. Trong số các hình học cơ bản như tam giác, tứ giác, và hình chữ nhật, hình bình hành là một trong những khái niệm mà học sinh thường gặp phải. Bài viết này sẽ giúp các bạn hiểu rõ hơn về khái niệm, tính chất và những cách chứng minh hình bình hành, từ đó hỗ trợ cho việc học tập và làm bài tập đạt hiệu quả cao hơn.
I. Khái Niệm Về Hình Bình Hành
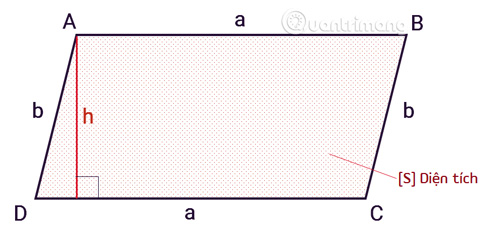
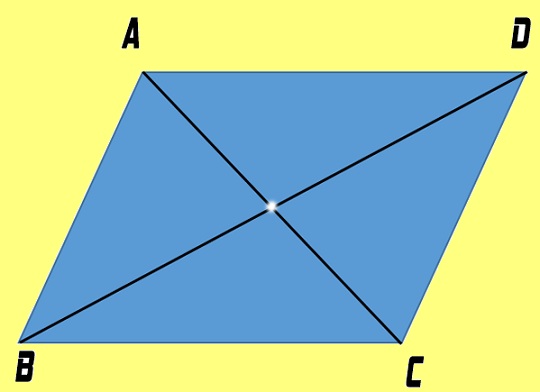
Hình bình hành là một tứ giác có các cặp cạnh đối song song. Từ khái niệm này, ta có thể định nghĩa rằng:
Tứ giác ABCD là hình bình hành nếu và chỉ nếu AB // CD và AD // BC.
Nhận Xét:
Hình bình hành là một hình thang có hai cạnh bên song song. Điều này cho thấy rằng hình bình hành là một trường hợp đặc biệt của hình thang.
II. Tính Chất Của Hình Bình Hành
Hình bình hành không chỉ có khái niệm đơn giản mà còn có nhiều tính chất quan trọng mà các bạn cần nắm rõ:
- Tính Chất 1: Trong hình bình hành, các cạnh đối bằng nhau.
Ví dụ: Nếu ABCD là hình bình hành thì AB = CD và AD = BC.
- Tính Chất 2: Trong hình bình hành, các góc đối bằng nhau.
Ví dụ: Nếu ABCD là hình bình hành thì Góc A = Góc C và Góc B = Góc D.
- Tính Chất 3: Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
Ví dụ: Nếu ABCD là hình bình hành và AC cắt BD tại O thì OA = OC và OB = OD.
III. Các Cách Chứng Minh Tứ Giác Là Hình Bình Hành
Cách 1: Tứ Giác Có Các Cạnh Đối Song Song
Một trong những cách chứng minh hình bình hành đơn giản nhất là chứng minh rằng các cặp cạnh đối song song.
Ví Dụ 1:
Cho tứ giác ABCD có E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
- EF là đường trung bình của tam giác ABC, do đó EF // AC.
- HG là đường trung bình của tam giác ACD, do đó HG // AC.
- Từ đó suy ra HG // EF.
- FG là đường trung bình của tam giác CBD, do đó FG // BD.
- HE là đường trung bình của tam giác ABD, do đó HE // BD.
Từ cả hai cặp cạnh song song, ta có tứ giác EFGH là hình bình hành.
Ví Dụ 2:
Cho hình bình hành ABCD (AB > BC). Tia phân giác góc D cắt AB ở E, tia phân giác góc B cắt CD ở F. Chứng minh DEBF là hình bình hành.
- Góc B1 = D1 do đều bằng một nửa của hai góc bằng nhau B và D trong hình bình hành ABCD.
- AB // CD, do đó Góc B1 = F1 (so le trong).
- Hai góc này lại ở vị trí đồng vị, suy ra DE // BF.
Xét tứ giác DEBF, ta có DE // BF và BE // DF, do đó tứ giác DEBF là hình bình hành.
Cách 2: Tứ Giác Có Các Cạnh Đối Bằng Nhau
Nếu một tứ giác có các cặp cạnh đối bằng nhau, ta có thể chứng minh nó là hình bình hành.
Ví Dụ 3:
Cho tứ giác ABCD có ΔABC = ΔCDA. Chứng minh rằng ABCD là hình bình hành.
- Từ việc ΔABC = ΔCDA, ta có AD = BC và AB = CD.
- Điều này cho thấy ABCD là hình bình hành.
Cách 3: Tứ Giác Có Hai Cạnh Đối Song Song Và Bằng Nhau
Nếu một tứ giác có hai cặp cạnh đối vừa song song vừa bằng nhau, thì nó là hình bình hành.
Ví Dụ 4:
Cho hình bình hành ABCD, gọi E là trung điểm AD, F là trung điểm BC. Chứng minh rằng BEDF là hình bình hành.
- Bởi vì ABCD là hình bình hành, ta có AD // BC và AD = BC.
- Do đó DE // BF (1).
- E là trung điểm AD, nên DE = AD/2.
- F là trung điểm BC, nên BF = BC/2.
- Vì AD = BC, suy ra DE = BF (2).
Từ (1) và (2), tứ giác DEBF là hình bình hành.
Cách 4: Tứ Giác Có Các Góc Đối Bằng Nhau
Nếu một tứ giác có các góc đối bằng nhau, ta cũng có thể chứng minh nó là hình bình hành.
Ví Dụ 5:
Cho tứ giác ABCD có ΔABC = ΔADC và ΔBAD = ΔBCD. Chứng minh rằng ABCD là hình bình hành.
- Từ ΔABC = ΔADC, ta có Góc ABC = Góc ADC (1).
- Từ ΔBAD = ΔBCD, ta có Góc BAD = Góc BCD (2).
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành.
Cách 5: Tứ Giác Có Hai Đường Chéo Cắt Nhau Tại Mỗi Trung Điểm
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường cũng là hình bình hành.
Ví Dụ 6:
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Từ A kẻ AE vuông góc với BD, từ C kẻ CF vuông góc với BD. Chứng minh rằng tứ giác AECF là hình bình hành.
- OA = OC (tính chất hình bình hành) (1).
- Xét hai tam giác vuông AEO và CFO:
- Góc AEO = Góc CFO = 90°.
- OA = OC.
- Góc AOE = Góc COF (đối đỉnh).
Từ đó, ΔAEO = ΔCFO (cạnh huyền - góc nhọn) suy ra OE = OF (2).
Từ (1) và (2) suy ra tứ giác AECF là hình bình hành.
Ví Dụ 7:
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng: AK // CI và DM = MN = NB.
- AB // CD và AB = CD (do ABCD là hình bình hành).
- I, K lần lượt là trung điểm AB, CD nên AI = IB và DK = KC.
- Tứ giác AICK có cặp cạnh đối song song và bằng nhau (AI và KC) nên AICK là hình bình hành, do đó AK // CI (điều phải chứng minh).
Tiếp theo, ta có AM // IN và MK // NC.
Xét tam giác AMB có AM // IN, AI = BI (I là trung điểm AB), IN là đường trung bình của tam giác AMB, N là trung điểm MB => MN = NB (1).
Tương tự, xét tam giác DNC có MK // NC, DK = CK (K là trung điểm DC), MK là đường trung bình của tam giác DNC, M là trung điểm DN => DM = NM (2).
Từ (1) và (2), suy ra DM = MN = NB.
Lời Kết
Bài viết trên đã tổng hợp các khái niệm, tính chất và cách chứng minh tứ giác là hình bình hành một cách rõ ràng và dễ hiểu. Đây là những kiến thức nền tảng mà học sinh sẽ thường xuyên gặp trong quá trình học tập hình học. Hi vọng rằng các bạn sẽ có thêm kiến thức bổ ích để làm bài tập hiệu quả hơn không chỉ với hình bình hành, mà còn với các phần khác trong môn hình học.
Các bạn hãy tiếp tục đồng hành cùng
Gia Sư Việt để nắm vững kiến thức và thực hành nhiều bài tập hơn nhé!
Tham Khảo Thêm:
- Giải pháp khắc phục tình trạng “mất gốc Hóa” hiệu quả nhất.
- Phương pháp học 7 hằng đẳng thức đáng nhớ hiệu quả nhất.
- Định nghĩa, tính chất & cách chứng minh các tam giác đặc biệt.
Hy vọng bài viết này sẽ là tài liệu hữu ích cho các bạn trong quá trình học tập và ôn luyện!