Hình bình hành là một trong những khái niệm cơ bản trong hình học. Việc nắm rõ công thức tính diện tích và chu vi của hình bình hành không chỉ giúp bạn trong học tập mà còn có ứng dụng trong nhiều lĩnh vực khác nhau. Trong bài viết này, chúng ta sẽ cùng khám phá chi tiết về cách tính diện tích hình bình hành và những điều cần biết về loại hình này.
1. Tìm Hiểu Về Hình Bình Hành
1.1 Định Nghĩa Hình Bình Hành
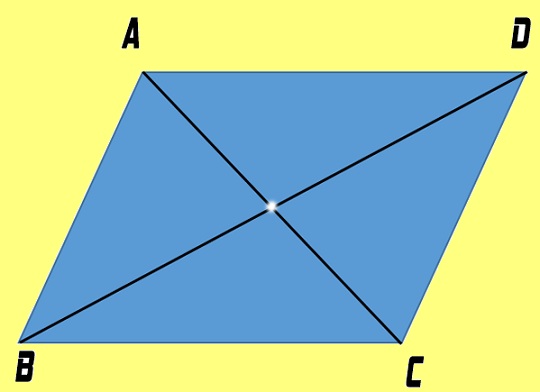
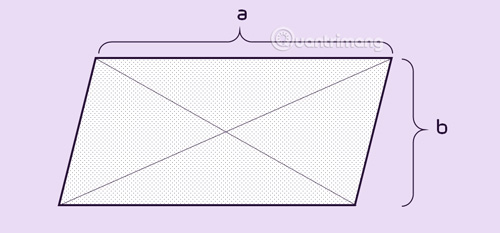
Hình bình hành là một tứ giác có hai cặp cạnh đối song song. Điều này có nghĩa là mỗi cặp cạnh đối không chỉ song song mà còn có độ dài bằng nhau. Hình bình hành có một số đặc điểm nổi bật như:
- Hai góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành được xem là một trường hợp đặc biệt của hình thang.
1.2 Tính Chất Của Hình Bình Hành
Trong hình bình hành, một số tính chất quan trọng bao gồm:
- Các cạnh đối bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
1.3 Dấu Hiệu Nhận Biết Hình Bình Hành
Để nhận biết hình bình hành, bạn có thể dựa vào các dấu hiệu sau:
- Tứ giác có các cạnh đối song song.
- Tứ giác có các cạnh đối bằng nhau.
- Tứ giác có hai cạnh đối song song và bằng nhau.
- Tứ giác có các góc đối bằng nhau.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường.
2. Công Thức Tính Diện Tích Hình Bình Hành
2.1 Diện Tích Hình Bình Hành
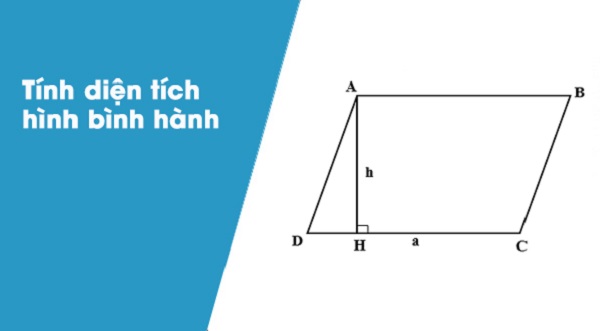
Diện tích hình bình hành được tính theo công thức:
```
S = a x h
```
Trong đó:
- S là diện tích hình bình hành.
- a là độ dài của cạnh đáy.
- h là chiều cao, là khoảng cách từ đỉnh đến cạnh đáy.
2.2 Ví Dụ Tính Diện Tích
Giả sử, bạn có một hình bình hành với cạnh đáy dài 10 cm và chiều cao 6 cm. Ta có thể tính diện tích như sau:
```
S = 10 x 6 = 60 cm²
```
3. Công Thức Tính Chu Vi Hình Bình Hành
3.1 Chu Vi Hình Bình Hành
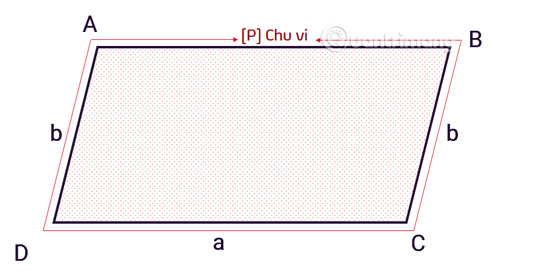
Chu vi hình bình hành được tính bằng công thức:
```
C = 2 x (a + b)
```
Trong đó:
- C là chu vi hình bình hành.
- a và b là độ dài của hai cạnh kề nhau.
3.2 Ví Dụ Tính Chu Vi
Giả sử, bạn có một hình bình hành với cạnh đáy dài 8 cm và cạnh bên dài 5 cm. Ta có thể tính chu vi như sau:
```
C = 2 x (8 + 5) = 26 cm
```
4. Tình Huống Áp Dụng Công Thức
4.1 Ví Dụ Về Tính Chu Vi Và Diện Tích
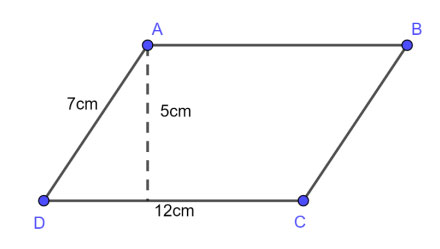
Ví dụ 1: Cho hình bình hành có cạnh đáy bằng 12 cm, cạnh bên bằng 7 cm, chiều cao bằng 5 cm. Hãy tính chu vi và diện tích của hình bình hành đó.
```
C = 2 x (12 + 7) = 38 cm
```
```
S = 12 x 5 = 60 cm²
```
4.2 Một Tình Huống Khác
Ví dụ 2: Xét hình bình hành ABCD với chiều cao từ đỉnh A đến cạnh đáy BC. Nếu chiều cao là 4 cm và cạnh đáy BC dài 10 cm, ta tính được diện tích:
```
S = 10 x 4 = 40 cm²
```
5. Câu Hỏi Trắc Nghiệm Về Hình Bình Hành
5.1 Câu Hỏi 1
Hãy chọn câu sai.
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
B. Hình bình hành có hai góc đối bằng nhau.
C. Hình bình hành có hai đường chéo vuông góc với nhau.
D. Hai bình hành có hai cặp cạnh đối song song.
Lời giải: Trong hình bình hành, hình bình hành có các cạnh đối song song, các cạnh đối bằng nhau, và hai đường chéo cắt nhau tại trung điểm của mỗi đường, do đó câu C là sai.
5.2 Câu Hỏi 2
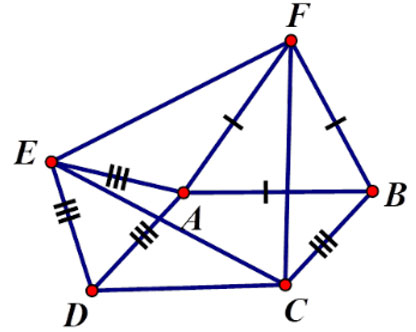
Cho hình bình hành ABCD có Â = α > 90°. Ở phía ngoài hình bình hành vẽ các tam giác đều ADE, ABF. Tam giác CEF là tam giác gì? Chọn câu trả lời đúng nhất.
A. Tam giác
B. Tam giác cân
C. Tam giác đều
D. Tam giác tù
Đáp án: Tam giác CEF là tam giác đều.
6. Ứng Dụng Của Công Thức Tính Diện Tích và Chu Vi Hình Bình Hành
Việc nắm vững công thức tính diện tích và chu vi hình bình hành không chỉ có ý nghĩa trong học tập mà còn rất thiết thực trong cuộc sống hàng ngày. Chẳng hạn, khi bạn cần tính diện tích một mảnh đất hình bình hành hay một bức tranh có hình dạng tương tự, bạn có thể áp dụng công thức này một cách dễ dàng.
7. Kết Luận
Hy vọng qua bài viết này, bạn đã nắm vững công thức tính diện tích hình bình hành cũng như cách tính chu vi của loại hình này. Hiểu rõ về hình bình hành không chỉ giúp bạn trong học tập mà còn trang bị cho bạn những kiến thức cần thiết để ứng dụng vào thực tế. Nếu bạn có bất kỳ câu hỏi nào liên quan đến hình bình hành hay các vấn đề khác trong hình học, hãy để lại câu hỏi trong phần bình luận bên dưới!