Hình thang là một trong những hình học cơ bản trong chương trình học toán, đặc biệt là ở cấp Trung học cơ sở và cao hơn. Với hai cạnh song song, hình thang không chỉ là một khái niệm đơn thuần mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Trong bài viết này, chúng ta sẽ tìm hiểu chi tiết về hình thang, tập trung vào cách tính
diện tích hình thang cân và các công thức liên quan.
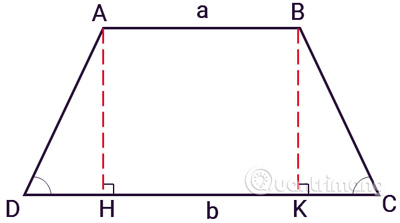
Hình Thang Là Gì?
Hình thang là một tứ giác lồi có hai cạnh song song, được gọi là các cạnh đáy, trong khi các cạnh còn lại được gọi là cạnh bên. Để tính được các thông số của hình thang, chúng ta cần nắm rõ các khái niệm cơ bản như chiều cao, độ dài các cạnh đáy và các cạnh bên.
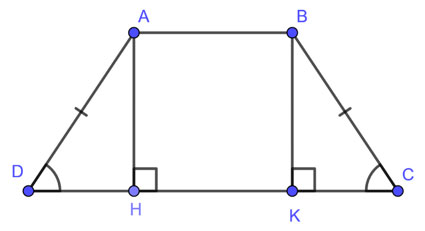
Công Thức Tính Diện Tích Hình Thang
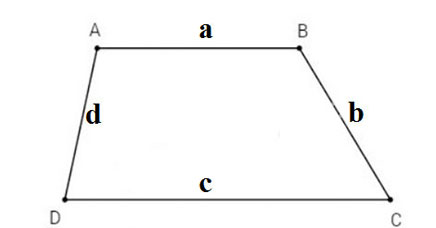
Công Thức Cơ Bản
Để tính diện tích của một hình thang, ta có công thức sau:
\[ S = \frac{(a + b) \times h}{2} \]
Trong đó:
- \( S \) là diện tích hình thang.
- \( a \) và \( b \) lần lượt là độ dài của hai đáy.
- \( h \) là chiều cao, tức là khoảng cách giữa hai đáy.
Ví Dụ Tính Diện Tích Hình Thang
Giả sử chúng ta có hình thang với đáy lớn \( a = 18 \, \text{cm} \), đáy nhỏ \( b = 14 \, \text{cm} \), và chiều cao \( h = 9 \, \text{cm} \). Áp dụng công thức:
\[ S = \frac{(18 + 14) \times 9}{2} = \frac{32 \times 9}{2} = 144 \, \text{cm}^2 \]
Diện Tích Hình Thang Cân
Đặc Điểm Của Hình Thang Cân
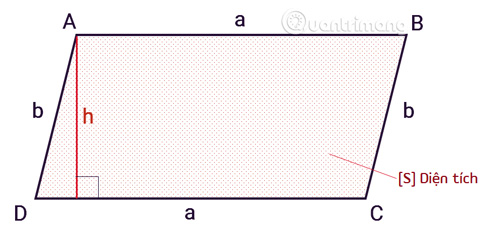
Hình thang cân là một loại hình thang đặc biệt, trong đó hai cạnh bên bằng nhau và hai góc kề một đáy bằng nhau. Hình thang cân không chỉ có vẻ đẹp đối xứng mà còn có những tính chất hình học thú vị. Để tính diện tích hình thang cân, ta cũng có thể áp dụng công thức tính diện tích hình thang thông thường.
Công Thức Tính Diện Tích Hình Thang Cân
Diện tích hình thang cân vẫn được tính theo công thức:
\[ S = \frac{(a + b) \times h}{2} \]
Tuy nhiên, trong trường hợp hình thang cân, chiều cao có thể được xác định thông qua các cạnh bên và đáy.
Cách Tính Cụ Thể
Giả sử hình thang cân ABCD có đáy lớn \( a \) và đáy nhỏ \( b \), và chiều cao \( h \) được xác định từ các cạnh bên. Chúng ta có thể tính diện tích bằng cách chia hình thang thành các phần đơn giản hơn.
- Chia Hình Thang Thành Hình Chữ Nhật và Hình Tam Giác:
- Ta có thể chia hình thang cân thành một hình chữ nhật và hai hình tam giác. Hình chữ nhật sẽ có độ dài bằng đáy lớn và chiều cao bằng chiều cao của hình thang. Hai hình tam giác sẽ có chiều cao bằng chiều cao của hình thang.
- Diện tích hình chữ nhật: \( S_{hcn} = a \times h \)
- Diện tích mỗi tam giác: \( S_{tg} = \frac{b \times h}{2} \)
- Tổng diện tích hình thang:
\[
S = S_{hcn} + 2 \times S_{tg} = a \times h + 2 \times \frac{b \times h}{2} = a \times h + b \times h = (a + b) \times h
\]
Ví Dụ Tính Diện Tích Hình Thang Cân
Giả sử hình thang cân có các thông số như sau:
- Đáy lớn \( a = 10 \, \text{cm} \)
- Đáy nhỏ \( b = 6 \, \text{cm} \)
- Chiều cao \( h = 4 \, \text{cm} \)
Áp dụng công thức:
\[ S = \frac{(10 + 6) \times 4}{2} = \frac{16 \times 4}{2} = 32 \, \text{cm}^2 \]
Các Dạng Toán Tính Diện Tích Hình Thang Cân
Ví Dụ 1: Tính Diện Tích Hình Thang Cân
Tính diện tích hình thang cân khi biết đáy lớn, đáy nhỏ và chiều cao.
- Đáy lớn: 24 cm
- Đáy nhỏ: 18 cm
- Chiều cao: 5 cm
Giải:
\[ S = \frac{(24 + 18) \times 5}{2} = \frac{42 \times 5}{2} = 105 \, \text{cm}^2 \]
Ví Dụ 2: Tính Diện Tích Mảnh Đất Hình Thang
Có một mảnh đất hình thang với đáy bé là 20 m, đáy lớn là 30 m. Hãy tính diện tích của mảnh đất nếu chiều cao là 10 m.
Giải:
\[ S = \frac{(20 + 30) \times 10}{2} = \frac{50 \times 10}{2} = 250 \, \text{m}^2 \]
Ví Dụ 3: Tìm Chiều Cao Khi Biết Diện Tích và Đáy
Cho diện tích hình thang là 200 cm², đáy lớn là 40 cm, đáy nhỏ là 20 cm. Tìm chiều cao của hình thang.
Giải:
Áp dụng công thức tính diện tích:
\[ 200 = \frac{(40 + 20) \times h}{2} \]
Giải cho \( h \):
\[ 200 = \frac{60 \times h}{2} \]
\[ 400 = 60h \]
\[ h = \frac{400}{60} = \frac{20}{3} \approx 6.67 \, \text{cm} \]
Kết Luận
Hình thang là một khái niệm hình học cơ bản nhưng rất phong phú và ứng dụng. Việc nắm vững các công thức tính diện tích, đặc biệt là diện tích hình thang cân, sẽ giúp bạn giải quyết được nhiều bài toán trong môn toán cũng như trong thực tế. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về hình thang và các công thức liên quan đến diện tích hình thang cân. Hãy áp dụng kiến thức này vào thực tế và luyện tập nhiều hơn nữa để có thể giải quyết các bài toán một cách nhanh chóng và chính xác!