Các Trường Hợp Bằng Nhau Của Tam Giác Vuông

Tam giác vuông là một trong những hình học cơ bản và quan trọng trong toán học. Hiểu rõ về các trường hợp bằng nhau của tam giác vuông không chỉ giúp học sinh nắm vững kiến thức hình học mà còn hỗ trợ trong việc giải quyết các bài tập. Trong bài viết này, chúng ta sẽ tìm hiểu chi tiết về các trường hợp bằng nhau của tam giác vuông, từ khái niệm cho đến các ví dụ minh họa cụ thể.

1. Hai Tam Giác Bằng Nhau Là Gì?

Hai tam giác được coi là bằng nhau khi chúng có các cạnh và góc tương ứng bằng nhau. Kí hiệu sự bằng nhau của hai tam giác ABC và DFE có thể được viết như sau: ΔABC = ΔDFE Trong đó:

• Các cặp cạnh tương ứng: AB = DE, AC = DF, BC = EF
• Các cặp góc tương ứng: ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

2. Các Trường Hợp Bằng Nhau Của Tam Giác Vuông

Tam giác vuông là một loại tam giác có một góc bằng 90 độ. Chính vì đặc điểm này, khi so sánh hai tam giác vuông, chúng ta có thể sử dụng một số điều kiện đặc biệt để chứng minh tính chất bằng nhau của chúng. Dưới đây là các trường hợp cụ thể:

2.1 Hai Cạnh Góc Vuông

Hai tam giác vuông được gọi là bằng nhau nếu hai cạnh liền kề góc vuông của tam giác này bằng với hai cạnh liền kề góc vuông của tam giác kia. Điều này có thể được diễn giải như sau:

• Cạnh - góc - cạnh

Ví dụ:

Giả sử có hai tam giác vuông ABC và DEF, với AB = DE, AC = DF. Ta có ΔABC = ΔDEF.

2.2 Cạnh Góc Vuông Và Góc Nhọn Liền Kề Cạnh Đó

Hai tam giác vuông bằng nhau cũng có thể được xác định nếu một cạnh góc vuông và một góc nhọn kề bên cạnh đó của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia. Điều này được gọi là:

• Góc - cạnh - góc

Ví dụ:

Nếu tam giác ABC có góc A = 90°, ∠B = β và cạnh AC = DF, thì ΔABC = ΔDEF khi ∠B = ∠E.

2.3 Cạnh Huyền Và Góc Nhọn

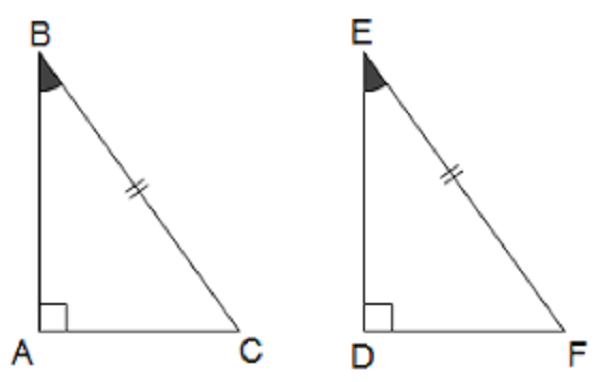
Một trường hợp nữa để hai tam giác vuông bằng nhau là khi một góc nhọn và cạnh huyền của tam giác vuông này bằng một góc nhọn và cạnh huyền của tam giác vuông kia. Điều này được diễn tả như sau:

• Góc - cạnh - góc

Ví dụ:

Giả sử tam giác ABC có cạnh huyền AB = DE và góc B = ∠E, thì ΔABC = ΔDEF.

2.4 Cạnh Huyền Và Cạnh Góc Vuông

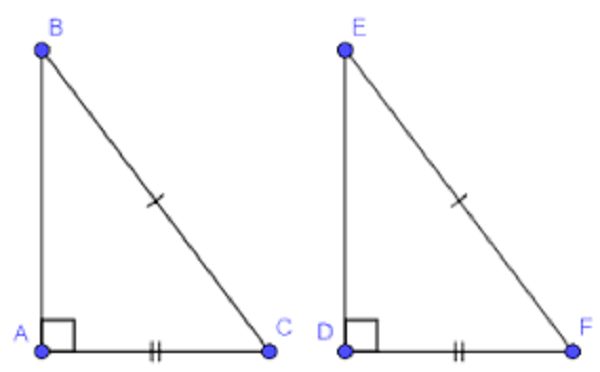
Cuối cùng, hai tam giác vuông cũng có thể bằng nhau nếu một cạnh của góc vuông và cạnh huyền của tam giác vuông này bằng một cạnh của góc vuông và cạnh huyền của tam giác vuông kia. Điều này có thể được diễn tả như:

• Cạnh huyền - cạnh góc vuông

Ví dụ:

Nếu tam giác ABC có cạnh huyền AB = DE và một cạnh góc vuông AC = DF, thì ΔABC = ΔDEF.

3. Các Dạng Bài Về Các Trường Hợp Bằng Nhau Của Tam Giác Vuông

Khi hiểu rõ các trường hợp bằng nhau của tam giác vuông, học sinh có thể giải quyết nhiều dạng bài khác nhau. Dưới đây là một số dạng bài phổ biến:

3.1 Dạng 1: Chứng Minh Các Tam Giác Vuông Bằng Nhau

Trong dạng này, học sinh cần xét và kiểm tra các điều kiện bằng nhau như cạnh - góc - cạnh, góc - cạnh - góc, cạnh huyền - góc nhọn hoặc cạnh huyền - cạnh góc vuông để đưa ra kết luận.

3.2 Dạng 2: Chứng Minh Góc Và Đoạn Thẳng Bằng Nhau

Đối với dạng bài này, học sinh sẽ vận dụng kiến thức về các trường hợp bằng nhau của hai tam giác vuông để chứng minh rằng nếu hai tam giác bằng nhau thì các đoạn thẳng và góc tương ứng cũng sẽ bằng nhau.

3.3 Dạng 3: Tìm Thêm Các Điều Kiện Để Hai Tam Giác Vuông Bằng Nhau

Dạng bài này yêu cầu học sinh đọc kỹ đề bài và vẽ hình để xem các yếu tố nào đã bằng nhau và cần bổ sung thêm điều kiện nào để hai tam giác vuông có thể bằng nhau.

4. Giải Một Số Ví Dụ Minh Họa Các Trường Hợp Bằng Nhau Của Tam Giác

Ví dụ 1

Cho tam giác MNP cân tại M. Kẻ MH vuông góc với NP. Chứng minh:

• a) HN = HP
• b) góc NMH = góc PMH

Trả lời:

• a) Xét hai tam giác vuông ΔMNH và ΔMPH, ta có MN = MP theo giả thiết và AH là cạnh chung. Suy ra: ΔMNH = ΔMPH theo trường hợp cạnh huyền - cạnh góc vuông. Suy ra HN = HP (cặp cạnh tương ứng).
• b) Từ ΔMNH = ΔMPH (chứng minh trên), suy ra góc NMH = góc PMH.

Ví dụ 2

Các tam giác vuông ABC và MNP có góc A và góc M bằng nhau và bằng 90 độ, AC = MP. Hãy thêm một điều kiện để hai tam giác ΔABC = ΔMNP. Bài giải: Nếu thêm AB = MN thì ta sẽ có hai tam giác ΔABC = ΔMNP theo trường hợp cạnh - góc - cạnh. Nếu thêm góc C = góc P thì ta sẽ có ΔABC = ΔMNP theo trường hợp góc - cạnh - góc. Khi thêm BC = NP thì ta sẽ có ΔABC = ΔMNP theo trường hợp cạnh huyền - cạnh góc vuông.

Ví dụ 3

Cho tam giác DEF cân tại điểm D, góc D nhỏ hơn 90°. Vẽ EK ⊥ DF (K ∈ DF), CH ⊥ DE (H ∈ DE).

• a) Chứng minh rằng DK = KH
• b) Gọi M là giao điểm của EK và CH. Chứng minh rằng đoạn thẳng DM chính là tia phân giác của góc D.

Bài giải:

• a) Giả thiết ΔDEF cân tại D thì có DE = DF. Xét hai tam giác vuông KDE và HDF, ta có DE = DF (chứng minh trên), góc D chung. ⇒ ΔKDE = ΔHDF theo (cạnh huyền - góc nhọn). ⇒ DK = DH (cặp cạnh tương ứng).
• b) Xét hai tam giác vuông HDM và KDM, ta có DK = DH (chứng minh trên), DM là cạnh chung, từ đó suy ra ΔKDM = ΔHDM (cạnh huyền - cạnh góc vuông) và cặp góc tương ứng là góc KDM = góc HDM. Vậy tia DM chính là tia phân giác của góc D.

5. Tổng Hợp Các Dạng Bài Tập Tam Giác Vuông Bằng Nhau

Dưới đây là tổng hợp các dạng bài tập lý thuyết và thực hành về các trường hợp bằng nhau của tam giác vuông.

5.1 Bài Tập Lý Thuyết

Bài 1: Hãy nêu các trường hợp bằng nhau của tam giác vuông? Vẽ hình ảnh minh họa cho từng trường hợp? Bài 2: Phát biểu định lý hai đường thẳng cùng vuông góc với một đường thẳng? Nêu giả thiết, kết luận? Vẽ hình minh họa. Bài 3: Nêu khái niệm hai tam giác bằng nhau? Vẽ hình minh họa.

5.2 Bài Tập Thực Hành

Bài 1: Cho tam giác ABC và tam giác DEF biết góc A = góc D = 90°, góc C = góc F. Cần bổ sung thêm điều kiện gì để hai tam giác ABC và DEF bằng nhau theo trường hợp cạnh góc vuông - góc nhọn kề?

• A. AC = DF
• B. AB = DE
• C. BC = EF
• D. AC = DE

Bài 2: Cho tam giác ABC và tam giác DEF có góc B và góc E bằng nhau và bằng 90°, AC = DF, góc A = góc F. Hãy tìm phát biểu đúng trong những phát biểu sau đây?

• A. ΔABC = ΔFED
• B. ΔABC = ΔFDE
• C. ΔBAC = ΔFED
• D. ΔABC = ΔDEF

Bài 3: Cho tam giác ABC, kẻ BE và CD lần lượt là đường cao vuông góc với các cạnh AC, AB. Chứng minh rằng hai tam giác BCD và CBE bằng nhau, biết BD = EC. Bài 4: Cho tam giác ACD cân tại A. Từ đỉnh A kẻ AH vuông góc với CD, H thuộc CD. Chứng minh rằng: HB = HC và AH là tia phân giác của góc BAC. Bài 5: Cho hai tam giác ABC và DEF lần lượt vuông tại A và D, biết AB = DE.

• a) Để hai tam giác trên có thể bằng nhau theo trường hợp cạnh góc vuông và góc nhọn kề thì cần thêm điều kiện gì?
• b) Để hai tam giác trên có thể bằng nhau theo trường hợp cạnh huyền và góc nhọn kề thì cần thêm điều kiện gì?

--- Trên đây là tổng hợp các thông tin liên quan đến các trường hợp bằng nhau của tam giác vuông và một số bài tập mà bạn có thể vận dụng. Hy vọng những kiến thức này sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán hình học về tam giác vuông. Chúc bạn học tốt!