Hình chóp cụt đều là một trong những khái niệm quan trọng trong hình học không gian. Trong bài viết này, chúng ta sẽ cùng nhau khám phá chi tiết về hình chóp cụt đều, cách tính thể tích, diện tích xung quanh và toàn phần của nó. Những kiến thức này không chỉ hữu ích cho các bạn học sinh, sinh viên mà còn cho những ai yêu thích toán học.
Định Nghĩa Hình Chóp Cụt
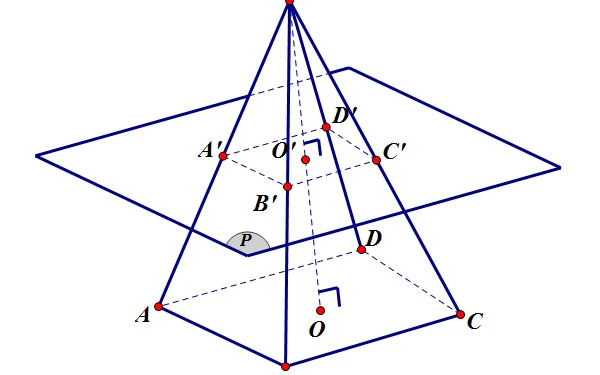
Hình chóp cụt là một phần của khối đa diện, nằm giữa mặt đáy và thiết diện cắt bởi mặt phẳng song song với đáy của hình chóp. Cụ thể hơn, hình chóp cụt được hình thành khi cắt đi phần trên của hình chóp bằng một mặt phẳng song song với mặt đáy.
Thành Phần Của Hình Chóp Cụt
Hình chóp cụt bao gồm những thành phần cơ bản như sau:
- Hai Đáy: Các đa giác A1A2...An và B1B2...Bn được gọi là hai mặt đáy của hình chóp cụt. Hai mặt đáy thường có kích thước và hình dạng khác nhau.
- Các Mặt Bên: Các hình thang A1A2B2B1, A2A3B3B2,..., AnA1B1Bn được gọi là các mặt bên của hình chóp cụt.
- Các Cạnh Bên: Các đoạn thẳng A1B1, A2B2,..., AnBn được gọi là các cạnh bên, trong khi các cạnh của mặt đáy được gọi là các cạnh đáy.
- Chiều Cao: Khoảng cách giữa hai mặt đáy được gọi là chiều cao của hình chóp cụt.
Tính Chất Của Hình Chóp Cụt
Hình chóp cụt đều có những đặc điểm nổi bật mà bạn cần lưu ý:
- Hai đáy là các đa giác có các cạnh tương ứng song song và tỉ số các cạnh tương ứng bằng nhau.
- Các mặt bên đều là các hình thang.
- Các đường thẳng chứa các cạnh bên sẽ đồng quy tại một điểm gọi là đỉnh của hình chóp.
- Hình chóp cụt đều có các mặt đáy là hình đa giác đều, do đó, các mặt bên cũng là những hình thang cân bằng nhau.
Công Thức Tính Diện Tích Hình Chóp Cụt
Diện Tích Xung Quanh Hình Chóp Cụt
Diện tích xung quanh của hình chóp cụt là tổng diện tích của tất cả các mặt bên, không bao gồm diện tích của hai mặt đáy. Để tính diện tích xung quanh, bạn cần tính diện tích từng mặt bên (các hình thang) và cộng chúng lại.
Công thức tính diện tích xung quanh của hình chóp cụt đều được xác định như sau:
\[ S_{xq} = \frac{(a + b) \cdot h}{2} \cdot n \]
Trong đó:
- \( S_{xq} \): Diện tích xung quanh
- \( n \): Số lượng mặt bên (bằng số cạnh của đa giác đáy)
- \( a \): Chiều dài cạnh của đáy lớn
- \( b \): Chiều dài cạnh của đáy nhỏ
- \( h \): Chiều cao của các mặt bên
Ví dụ Tính Diện Tích Xung Quanh Hình Chóp Cụt
Ví dụ 1: Tính diện tích xung quanh của hình chóp cụt có đáy lớn là 10cm, đáy nhỏ là 15cm, chiều cao của mặt bên là 12cm.
Giải:
\[ S = \frac{(10 + 15) \cdot 12}{2} = 150 \, (cm^2) \]
- Hình chóp cụt có 4 mặt bên, nên diện tích xung quanh là:
\[ S_{xq} = 150 \cdot 4 = 600 \, (cm^2) \]
Ví dụ 2: Tính diện tích xung quanh của hình chóp cụt với đáy lớn 6cm, đáy nhỏ 8cm và chiều cao mặt bên là 5cm.
Giải:
- Diện tích một mặt bên là:
\[ S = \frac{(6 + 8) \cdot 5}{2} = 35 \, (cm^2) \]
\[ S_{xq} = 35 \cdot 4 = 140 \, (cm^2) \]
Diện Tích Toàn Phần Của Hình Chóp Cụt
Diện tích toàn phần của hình chóp cụt được tính bằng tổng diện tích xung quanh và diện tích của hai mặt đáy. Công thức tính diện tích toàn phần là:
\[ S_{tp} = S_{xq} + S_{đáy \ lớn} + S_{đáy \ nhỏ} \]
Trong đó:
- \( S_{tp} \): Diện tích toàn phần
- \( S_{xq} \): Diện tích xung quanh
- \( S_{đáy \ lớn} \): Diện tích đáy lớn
- \( S_{đáy \ nhỏ} \): Diện tích đáy nhỏ
Ví dụ Tính Diện Tích Toàn Phần
Ví dụ: Tính diện tích toàn phần của hình chóp cụt vừa tính ở trên.
Giải:
\[ S_{đáy \ lớn} = 10 \cdot 10 = 100 \, (cm^2) \]
\[ S_{đáy \ nhỏ} = 15 \cdot 15 = 225 \, (cm^2) \]
\[ S_{tp} = 600 + 100 + 225 = 925 \, (cm^2) \]
Công Thức Tính Thể Tích Hình Chóp Cụt
Để tính thể tích của hình chóp cụt, bạn có thể sử dụng công thức sau:
\[ V = \frac{h}{3} (S + S') \]
Trong đó:
- \( V \): Thể tích hình chóp cụt
- \( S \): Diện tích mặt đáy lớn
- \( S' \): Diện tích mặt đáy nhỏ
- \( h \): Chiều cao của hình chóp, tức là khoảng cách giữa hai mặt đáy.
Ví dụ Tính Thể Tích Hình Chóp Cụt
Ví dụ: Tính thể tích hình chóp cụt với đáy lớn 10cm, đáy nhỏ 15cm và chiều cao 12cm.
Giải:
\[ S = 10 \cdot 10 = 100 \, (cm^2) \]
\[ S' = 15 \cdot 15 = 225 \, (cm^2) \]
\[ V = \frac{12}{3} (100 + 225) = 4 \cdot 325 = 1300 \, (cm^3) \]
Kết Luận
Hình chóp cụt đều không chỉ là một khái niệm thú vị trong hình học mà còn là một phần quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Việc hiểu rõ về định nghĩa, các thành phần, tính chất và các công thức tính toán liên quan đến hình chóp cụt sẽ giúp bạn phát triển tư duy toán học và ứng dụng thực tế một cách hiệu quả hơn.
Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin bổ ích và chi tiết về hình chóp cụt đều. Hãy thực hành những bài tập tính toán để nâng cao kỹ năng của mình nhé!
























