Hình thoi là một trong những khái niệm hình học cơ bản mà học sinh được làm quen từ những năm đầu học phổ thông. Không chỉ xuất hiện trong sách giáo khoa, hình thoi còn là một phần thiết yếu trong nhiều lĩnh vực như kiến trúc, thiết kế nội thất và nghệ thuật. Trong bài viết này, Cmath sẽ cùng bạn khám phá công thức tính chu vi hình thoi từ cơ bản đến nâng cao, giúp bạn hiểu rõ hơn về loại hình này.
Khái niệm và Đặc Điểm của Hình Thoi
Định Nghĩa Hình Thoi
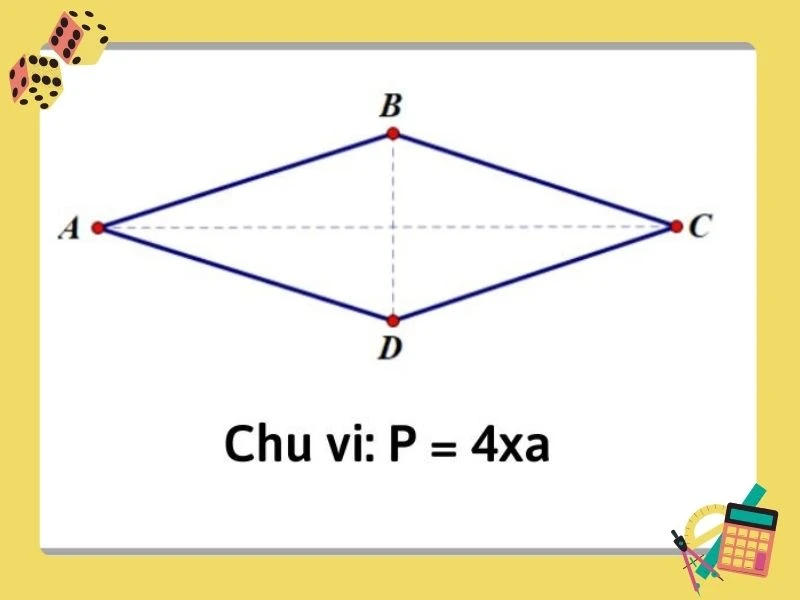
Hình thoi là một tứ giác có bốn cạnh bằng nhau. Đặc biệt hơn, nó còn được xem là một hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Hình thoi có những đặc điểm độc đáo khác biệt so với các hình khác, và đặc biệt là hình vuông. Nếu một hình thoi có bốn góc vuông, thì nó sẽ trở thành hình vuông. Do đó, hình vuông có thể được coi là một trường hợp đặc biệt của hình thoi.

Đặc Điểm Nổi Bật
- Bốn cạnh bằng nhau: Đây là đặc điểm quan trọng nhất của hình thoi. Mỗi cạnh đều có độ dài bằng nhau, tạo nên sự đối xứng hoàn hảo.
- Hai đường chéo cắt nhau: Các đường chéo của hình thoi cắt nhau vuông góc và chia đôi nhau tại trung điểm.
- Các góc đối bằng nhau: Tổng các góc trong hình thoi luôn bằng 360 độ, trong đó các góc đối có giá trị bằng nhau.
Tính Chất Chi Tiết của Hình Thoi
Hình thoi không chỉ đẹp về mặt hình học mà còn sở hữu nhiều tính chất thú vị như sau:
- Kế thừa tính chất hình bình hành: Hình thoi thừa hưởng tất cả các tính chất của hình bình hành, trong đó có các cạnh đối song song và bằng nhau.
- Đường chéo chia đôi góc: Mỗi đường chéo của hình thoi chia đôi góc mà nó đi qua, đồng nghĩa với việc các góc do một đường chéo tạo ra với hai cạnh kề sẽ bằng nhau.
- Có các trục đối xứng: Tất cả các cạnh của hình thoi đều là trục đối xứng. Điều này có nghĩa là nếu bạn gấp hình thoi dọc theo bất kỳ cạnh nào, hai nửa sẽ trùng khít lên nhau.
Công Thức Tính Chu Vi Hình Thoi
Công Thức Cơ Bản
Cách tính chu vi hình thoi được thực hiện đơn giản bằng cách tính tổng độ dài của bốn cạnh. Công thức cụ thể là:
\[ P = a \times 4 \]
Trong đó:
- \( P \) là chu vi hình thoi.
- \( a \) là chiều dài một cạnh bất kỳ của hình thoi.
Ví Dụ Minh Họa
Giả sử một hình thoi có độ dài mỗi cạnh là 5 cm, ta có:
\[ P = 5 \text{ cm} \times 4 = 20 \text{ cm} \]
Như vậy, chu vi của hình thoi đó là 20 cm.
Ứng Dụng Trong Thực Tiễn
Công thức tính chu vi hình thoi không chỉ đơn thuần là một lý thuyết mà còn được ứng dụng rộng rãi trong cuộc sống. Từ thiết kế kiến trúc đến trang trí nghệ thuật, việc tính toán chu vi hình thoi giúp các kỹ sư và nhà thiết kế có kế hoạch chính xác cho các dự án của mình.
Các Dạng Bài Tập Sử Dụng Công Thức Tính Chu Vi Hình Thoi
Dạng 1: Tính Chu Vi Khi Biết Độ Dài Cạnh
Dạng bài này là dạng đơn giản nhất. Chỉ cần áp dụng công thức \( P = 4 \times a \) là bạn đã có thể tính được chu vi hình thoi.
Dạng 2: Bài Toán Cho Biết Chu Vi, Tìm Độ Dài Một Cạnh
Khi bài toán yêu cầu tìm độ dài một cạnh khi đã biết chu vi, bạn cần thực hiện phép tính ngược lại:
\[ a = \frac{P}{4} \]
Ví Dụ: Tính độ dài mỗi cạnh của hình thoi ABCD, biết rằng chu vi của hình thoi này là 36 cm.
Giải:
Đặt \( a \) là độ dài các cạnh của hình thoi.
Theo công thức, chu vi hình thoi là:
\[ P = 4 \times a \]
Suy ra:
\[ a = \frac{36}{4} = 9 \text{ cm} \]
Do đó, độ dài mỗi cạnh của hình thoi ABCD là 9 cm.
Dạng 3: Tính Chu Vi Khi Biết Đường Chéo
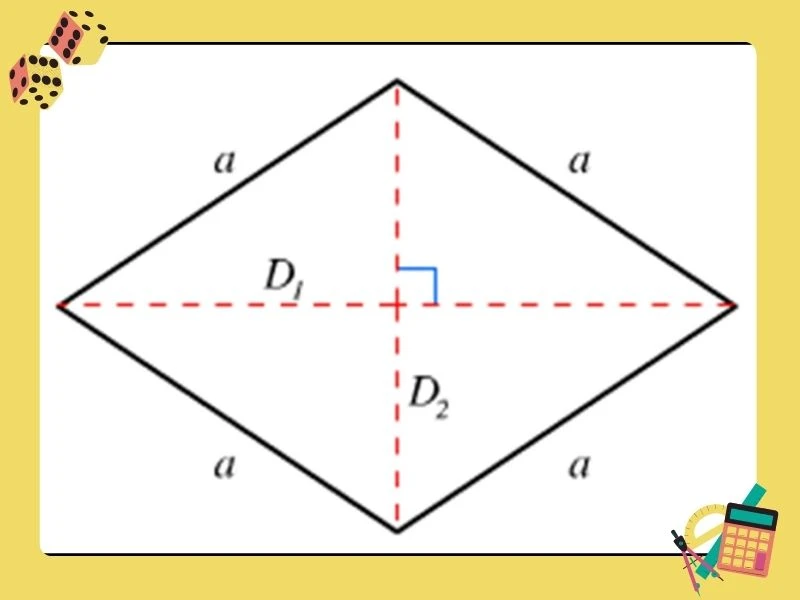
Khi chỉ biết độ dài các đường chéo, bạn có thể áp dụng định lý Pytago trong tam giác vuông:
\[ a^2 = \left(\frac{d_1}{2}\right)^2 + \left(\frac{d_2}{2}\right)^2 \]
Ví Dụ: Tính chu vi hình thoi biết độ dài hai đường chéo lần lượt là 16 cm và 30 cm.
Giải:
Gọi \( a \) là các cạnh của hình thoi, với \( d_1 = 16 \text{ cm} \) và \( d_2 = 30 \text{ cm} \).
Áp dụng định lý Pytago:
\[ a^2 = \left(\frac{16}{2}\right)^2 + \left(\frac{30}{2}\right)^2 = 8^2 + 15^2 = 64 + 225 = 289 \]
\[ a = \sqrt{289} = 17 \text{ cm} \]
Từ đó, chu vi của hình thoi là:
\[ P = 4 \times 17 = 68 \text{ cm} \]
Dạng 4: Bài Toán Kết Hợp Với Các Hình Học Khác
Hình thoi có thể xuất hiện trong các bài toán kết hợp với các hình khác như hình vuông, hình chữ nhật. Để giải quyết dạng bài này, bạn cần phân tích kỹ đề bài và xác định hình thoi, sau đó áp dụng đúng công thức.
Bài Tập Về Công Thức Tính Chu Vi Hình Thoi Tự Luyện Tại Nhà
Dưới đây là một số bài tập về cách tính chu vi hình thoi để bạn có thể tự luyện tập tại nhà:
- Bài Tập 1: Cho một hình thoi có độ dài một cạnh là 7 cm. Tính chu vi của hình thoi đó.
- Bài Tập 2: Cho một hình thoi có chu vi là 24 cm. Tính độ dài một cạnh của hình thoi đó.
- Bài Tập 3: Cho một hình vuông có cạnh dài 4 cm. Tính chu vi của hình thoi có độ dài hai đường chéo bằng với cạnh của hình vuông.
- Bài Tập 4: Cho một hình thoi có độ dài hai đường chéo lần lượt là 8 cm và 6 cm. Tính chu vi của hình thoi đó.
- Bài Tập 5: So sánh chu vi của hai hình thoi A và B, trong đó hình thoi A có cạnh dài 5 cm và hình thoi B có cạnh dài 7 cm.
Chinh Phục Các Bài Toán Tính Chu Vi Hình Thoi Nâng Cao Tại Cmath
Để nâng cao kỹ năng chinh phục các bài tập về chu vi hình thoi, các bạn nên tham khảo Trung tâm Toán tư duy Cmath. Tại đây, các học sinh sẽ được học tập theo chương trình giáo dục phổ thông mới nhất do Bộ GDĐT đưa ra, giúp các em phát triển toàn diện năng lực học tập.
Phương Pháp Giảng Dạy
Trung tâm Cmath áp dụng các phương pháp giảng dạy hiện đại, tập trung vào việc phát triển tư duy độc lập và khả năng tìm tòi, sáng tạo của trẻ. Đội ngũ giáo viên tại Cmath sẽ hướng dẫn trẻ tìm ra cách giải mới và hiệu quả nhất. Đến với Cmath, toán học sẽ không còn là một môn học khó nhằn mà trở thành người bạn đồng hành đáng tin cậy trên con đường học tập của các em.

Kết Luận
Thông qua bài viết này, chúng tôi hy vọng đã cung cấp cho bạn một cái nhìn chi tiết về
công thức tính chu vi hình thoi cùng với các ví dụ và bài tập thực hành để bạn có thể nắm vững kiến thức. Nếu cha mẹ đang tìm kiếm một phương pháp học toán hiện đại và hiệu quả cho trẻ, hãy liên hệ ngay với Cmath để được hỗ trợ và tư vấn nhanh chóng.
Xem Thêm
- Bật mí cách tính chu vi hình vuông chính xác, đơn giản nhất.
- Công thức tính chu vi hình chữ nhật chính xác và bài tập đi kèm.
- Công thức tính chu vi tam giác chuẩn, chính xác kèm bài tập.
Chúc bạn thành công trong việc chinh phục các bài toán hình học!



























