Trong bài viết trước, chúng ta đã tìm hiểu về cách tính tổng của hai vectơ. Hôm nay, chúng ta sẽ đi sâu vào một vấn đề thú vị hơn: Cách tìm tổng của hai vectơ có chung điểm đầu. Để làm điều này, chúng ta sẽ nhắc lại quy tắc ba điểm đã học, đồng thời giới thiệu thêm về một quy tắc mới mang tên
quy tắc hình bình hành. Bài viết này cũng sẽ tổng hợp một số bài toán liên quan để bạn đọc có thể dễ dàng áp dụng quy tắc này.
1. Nhắc lại Quy Tắc Ba Điểm
1.1. Định Nghĩa Tổng Của 2 Vectơ
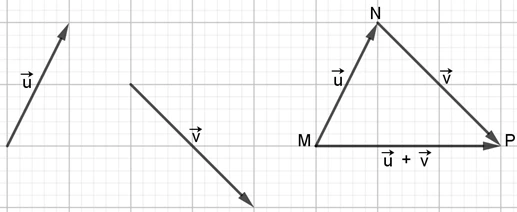
Cho hai vectơ \(\vec{u}\) và \(\vec{v}\). Chúng ta có thể chọn một điểm M bất kỳ và vẽ sao cho \(\vec{u}\) và \(\vec{v}\) bắt đầu từ M. Khi đó, vectơ \(\vec{w}\) được gọi là tổng của vectơ \(\vec{u}\) và \(\vec{v}\). Ký hiệu tổng của vectơ \(\vec{u}\) và \(\vec{v}\) là \(\vec{w} = \vec{u} + \vec{v}\). Như vậy, ta có:
\[
\vec{w} = \vec{u} + \vec{v}
\]
1.2. Quy Tắc Ba Điểm
Cho ba điểm M, N, P bất kỳ. Từ định nghĩa phép cộng vectơ, ta có đẳng thức vectơ như sau (quy tắc 3 điểm):
\[
\vec{u} + \vec{v} = \vec{MN} + \vec{NP}
\]
Chú ý rằng, để tìm tổng của hai vectơ theo quy tắc 3 điểm, ta cần biến đổi sao cho điểm cuối của vectơ thứ nhất trùng với điểm đầu của vectơ thứ hai.
Xem thêm:
2. Quy Tắc Hình Bình Hành Vectơ
Quy tắc hình bình hành là một công cụ mạnh mẽ trong việc tính toán tổng của hai vectơ. Cho hình bình hành MNPQ, ta có quy tắc sau:
\[
\vec{u} + \vec{v} = \vec{MP} + \vec{MQ}
\]
Chứng Minh Quy Tắc Hình Bình Hành
Vì MNPQ là hình bình hành, ta có thể suy ra (theo tính chất hai vectơ bằng nhau):
\[
\vec{MN} = \vec{PQ}
\]
Do đó, theo quy tắc 3 điểm, ta suy ra điều phải chứng minh:
\[
\vec{u} + \vec{v} = \vec{MP} + \vec{MQ}
\]
Ví Dụ 1: Tính Tổng Vectơ Trong Hình Bình Hành
Cho tứ giác GLXY là hình bình hành. Hãy sử dụng quy tắc hình bình hành đã học để tìm các tổng sau:
- \(\vec{GL} + \vec{LX}\)
- \(\vec{GX} + \vec{XY}\)
Lời giải:
- Sử dụng quy tắc hình bình hành, ta có:
\[
\vec{GL} + \vec{LX} = \vec{GX}
\]
- Sử dụng quy tắc hình bình hành, ta có:
\[
\vec{GX} + \vec{XY} = \vec{GY}
\]
Nhận Xét
Khi có hai vectơ và vectơ cùng chung điểm đầu, chúng ta sẽ sử dụng quy tắc hình bình hành để tìm tổng của chúng. Để tính tổng của hai vectơ bất kỳ, ta cần biến đổi chúng về tổng của hai vectơ có cùng chung điểm đầu, từ đó áp dụng quy tắc hình bình hành.
Ví Dụ 2: Tìm Tổng Hai Vectơ
Cho vectơ \(\vec{a}\) và vectơ \(\vec{b}\) trong hình vẽ sau. Hãy sử dụng quy tắc hình bình hành để tìm tổng của hai vectơ đó.
Lời giải:
Ta vẽ hình bình hành MNPQ sao cho \(\vec{a} = \vec{MP}\) và \(\vec{b} = \vec{MQ}\).
Khi đó, ta suy ra:
\[
\vec{a} + \vec{b} = \vec{MQ} + \vec{MP}
\]
Sử dụng quy tắc hình bình hành, ta được:
\[
\vec{a} + \vec{b} = \vec{MQ}
\]
Do đó:
\[
\vec{a} + \vec{b} = \vec{MP}
\]
3. Các Dạng Toán Áp Dụng Quy Tắc Hình Bình Hành
3.1. Dạng 1: Tính Độ Dài Của Tổng Hai Vectơ
Phương pháp giải:
Để tính độ dài của tổng hai vectơ bất kỳ, ta cần biến đổi tổng đó về tổng của hai vectơ có cùng chung điểm đầu, sau đó sử dụng quy tắc hình bình hành để tìm độ dài cụ thể của vectơ tổng.
Bài Tập Vận Dụng:
Bài 1: Cho tam giác MNP. Gọi điểm K là trung điểm của đoạn thẳng NP. Biết MK = u. Hãy tính độ dài của tổng hai vectơ sau:
\(\vec{MN} + \vec{MP}\)
Đáp án:
Gọi E là điểm đối xứng với điểm M qua điểm K.
Xét tứ giác MNEP có:
- \(MK = EK\) (do E là điểm đối xứng với M qua K)
- \(NK = PK\) (do K là trung điểm của đoạn thẳng NP)
Ta suy ra, tứ giác MNEP có hai đường chéo ME và NP cắt nhau tại trung điểm K.
Do đó tứ giác MNEP là hình bình hành.
Sử dụng quy tắc hình bình hành, ta được:
\[
\vec{MN} + \vec{MP} = \vec{ME}
\]
Ta có \(ME = 2MK = 2u\) (do E là điểm đối xứng với M qua K).
Vậy độ dài của tổng hai vectơ là \(2u\).
Bài 2: Cho ABCDRT là lục giác đều. Gọi điểm E là tâm của lục giác đều ABCDRT. Biết lục giác đều ABCDRT có độ dài các cạnh bằng 2 (đvđd). Hãy tính độ dài của tổng hai vectơ sau:
\(\vec{AE} + \vec{CE}\)
Đáp án:
Vì ABCDRT là lục giác đều với điểm E là tâm, nên ta có:
\[
\vec{AE} = \vec{CE}
\]
Lại có tứ giác AECG là hình bình hành, khi đó, sử dụng quy tắc hình bình hành, ta được:
\[
\vec{AE} + \vec{CE} = \vec{AC}
\]
Do đó, \(AC = 2\) (vì các cạnh đều có độ dài bằng 2).
Vậy độ dài của tổng hai vectơ là 2.
3.2. Dạng 2: Chứng Minh Đẳng Thức Vectơ
Phương pháp giải:
Để chứng minh đẳng thức vectơ, ta cần biến đổi vế phức tạp có chứa tổng của hai vectơ về tổng của hai vectơ có cùng chung điểm đầu, sau đó áp dụng quy tắc hình bình hành để chứng minh.
Bài Tập Vận Dụng:
Bài 4: Cho tứ giác GLXY là hình bình hành. Hãy chứng minh đẳng thức vectơ sau:
\(\vec{GL} + \vec{XY} = \vec{GX}\)
Đáp án:
Vì tứ giác GLXY là hình bình hành, nên ta có \(\vec{GL} = \vec{XY}\).
Khi đó, ta được:
\[
\vec{GL} + \vec{XY} = \vec{GX}
\]
Bài 5: Cho ABCDRT là lục giác đều. Hãy chứng minh đẳng thức vectơ sau:
\(\vec{AE} + \vec{CD} = \vec{AC}\)
Đáp án:
Vì ABCDRT là lục giác đều với điểm E là tâm, nên ta có \(\vec{AE} = \vec{CD}\).
Lại có tứ giác AECG là hình bình hành, sử dụng quy tắc hình bình hành, ta được:
\[
\vec{AE} + \vec{CD} = \vec{AC}
\]
Kết Luận
Qua chuyên đề
quy tắc hình bình hành vectơ, hy vọng rằng các bạn sẽ nắm vững quy tắc này và áp dụng chúng để xử lý các bài toán một cách sáng tạo và hiệu quả. Quy tắc hình bình hành không chỉ là một công cụ hữu ích trong toán học mà còn mở ra nhiều cơ hội để cải thiện khả năng tư duy logic và giải quyết vấn đề. Hãy tiếp tục luyện tập và khám phá thêm nhiều bài toán thú vị khác!
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang.
























