Hình cầu là một trong những đối tượng hình học cơ bản, không chỉ xuất hiện nhiều trong toán học mà còn trong tự nhiên và đời sống hàng ngày. Nếu bạn đang tìm kiếm kiến thức về diện tích hình cầu, công thức tính toán kèm theo các ví dụ cụ thể giúp bạn áp dụng vào thực tế, hãy cùng khám phá qua bài viết dưới đây.

I. Đặc Điểm Của Hình Cầu

1. Khái Niệm Về Hình Cầu
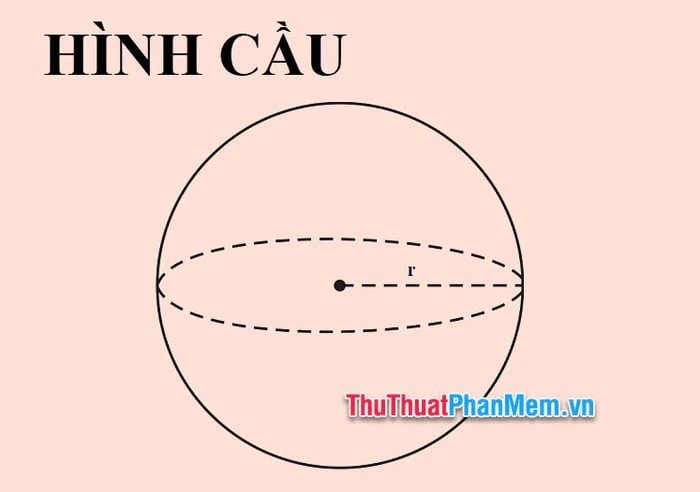
Hình cầu được định nghĩa là một hình thể tròn trong không gian ba chiều, nơi mà khoảng cách từ mọi điểm trên bề mặt đến một điểm trung tâm (hay còn gọi là tâm hình cầu) là một hằng số. Khoảng cách này được xác định là bán kính (R). Hình cầu có thể hình dung như là kết quả của việc quay một hình tròn quanh một trục đi qua tâm của nó.

2. Thành Phần Chính Của Hình Cầu
- Tâm hình cầu (O): Điểm trung tâm của hình cầu.
- Bán kính (R): Khoảng cách từ tâm đến bề mặt hình cầu.
- Đường kính (D): Kích thước lớn nhất của hình cầu, được tính bằng 2R.
II. Công Thức Tính Diện Tích Bề Mặt Hình Cầu
Công thức tính diện tích bề mặt của hình cầu được trình bày như sau:
1. Công Thức Cơ Bản
\[ S = 4\pi r^2 \]
Trong đó:
- S là diện tích bề mặt của hình cầu.
- π (Pi) là một hằng số, có giá trị khoảng 3.14159.
- r là bán kính của hình cầu.

2. Diện Tích Bề Mặt Nửa Hình Cầu
Khi tính diện tích của nửa hình cầu, công thức sẽ được điều chỉnh như sau:
\[ S_{nửa} = 2\pi r^2 + \pi r^2 = 3\pi r^2 \]
3. Hướng Dẫn Tính Bán Kính Từ Đường Kính
Khi bạn biết đường kính (D) của hình cầu, bán kính được tính bằng:
\[ r = \frac{D}{2} \]
Và bạn có thể thay thế giá trị bán kính vào công thức diện tích bề mặt.
III. Các Dạng Bài Tập Tính Diện Tích Bề Mặt Hình Cầu
1. Tính Diện Tích Khi Biết Bán Kính
Đây là dạng bài tập phổ biến nhất. Ví dụ, nếu bán kính của hình cầu là 5 cm, bạn dễ dàng tính được diện tích bề mặt bằng công thức:
\[ S = 4\pi (5^2) = 4\pi (25) = 100\pi \approx 314.16 \, cm^2 \]
2. Tính Diện Tích Khi Biết Đường Kính
Nếu đường kính của hình cầu là 12 cm, bạn tính bán kính và sau đó áp dụng công thức:
- Bán kính: \( r = \frac{12}{2} = 6 \, cm \)
- Diện tích: \( S = 4\pi (6^2) = 144\pi \approx 452.39 \, cm^2 \)
3. Tính Diện Tích Khi Biết Thể Tích
Khi có thể tích \( V \) của hình cầu:
\[ V = \frac{4}{3}\pi r^3 \]
Nếu \( V = 904 \, cm^3 \), bạn có thể suy luận bán kính:
- Bán kính: \( r = \sqrt[3]{\frac{3V}{4\pi}} = \sqrt[3]{\frac{3 \times 904}{4\pi}} \)
- Sau đó tính diện tích bằng công thức bề mặt.
IV. Ví Dụ Minh Họa Chi Tiết
Ví Dụ 1: Hình Cầu Có Bán Kính 6 cm
Đề bài: Cho hình cầu có bán kính là 6 cm, tính diện tích bề mặt.
Giải:
\[ S = 4\pi (6^2) = 4\pi (36) = 144\pi \approx 452.39 \, cm^2 \]
Ví Dụ 2: Hình Cầu Có Đường Kính 10 cm
Đề bài: Cho hình cầu có đường kính 10 cm, tìm diện tích bề mặt.
Giải:
- Tính bán kính: \( r = 5 \, cm \)
- Tính diện tích:
\[ S = 4\pi (5^2) = 4\pi (25) = 100\pi \approx 314.16 \, cm^2 \]
Ví Dụ 3: Hình Cầu Có Thể Tích 900 cm³
Đề bài: Hãy tính diện tích bề mặt hình cầu với thể tích \( V = 900 \, cm^3 \).
Giải:
- Tính bán kính từ thể tích:
\[ r = \sqrt[3]{\frac{3 \times 900}{4\pi}} \approx 6.34 \, cm \]
\[ S = 4\pi (6.34^2) \approx 505.91 \, cm^2 \]
V. Kết Luận
Hình cầu là một hình thể thú vị trong hình học với những ứng dụng phong phú trong toán học và thực tiễn. Việc hiểu rõ công thức tính diện tích bề mặt của hình cầu cùng với các dạng bài tập sẽ giúp bạn tự tin hơn trong việc giải quyết bài toán liên quan đến hình cầu. Hy vọng bài viết đã cung cấp cho bạn những kiến thức hữu ích và dễ hiểu để ứng dụng trong học tập cũng như công việc hàng ngày. Cảm ơn bạn đã theo dõi!






























