
1. Khối trụ tròn xoay là gì?
Khối trụ tròn xoay là một trong những khái niệm cơ bản trong hình học không gian. Được hình thành từ việc quay một hình phẳng quanh một trục cố định, khối trụ tròn xoay là kết quả của việc quay hình tròn quanh trục của nó. Hình trụ này không chỉ là bề mặt bên ngoài mà còn bao gồm cả không gian bên trong mà nó chiếm giữ.

Đặc điểm của khối trụ tròn xoay
- Đáy tròn: Khối trụ có hai đáy là hai đường tròn giống hệt nhau.
- Chiều cao: Khoảng cách giữa hai đáy tròn được gọi là chiều cao của khối trụ.
- Bán kính: Bán kính của mặt đáy là khoảng cách từ tâm đáy đến một điểm trên đường tròn.
Thể tích của khối trụ tròn xoay được xác định bởi lượng không gian mà nó chiếm và có thể được tính bằng một công thức cụ thể mà chúng tôi sẽ đề cập đến trong phần sau.
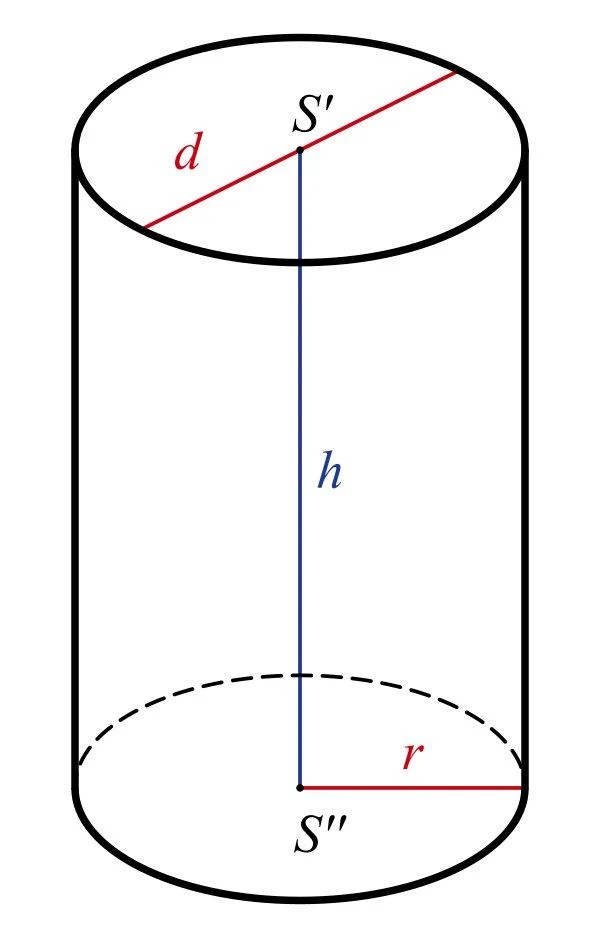
2. Công thức tính thể tích hình trụ tròn xoay
Để tính thể tích của khối trụ tròn xoay, chúng ta sử dụng công thức:
\[ V = \pi r^{2} h \]
Trong đó:
- \( V \) là thể tích của khối trụ.
- \( r \) là bán kính mặt đáy khối trụ.
- \( h \) là chiều cao của khối trụ.
- \( \pi \) là hằng số Pi, khoảng 3.14.
Giải thích công thức
Công thức trên cho thấy rằng thể tích của khối trụ tròn xoay là tích của diện tích mặt đáy (hình tròn) và chiều cao của khối trụ. Diện tích mặt đáy được tính bằng \( \pi r^{2} \), và khi nhân với chiều cao \( h \), chúng ta sẽ có thể tích của toàn bộ khối trụ.
Những điều cần lưu ý
- Đơn vị: Thể tích thường được đo bằng mét khối (m³).
- Tương tự với khối lăng trụ: Công thức tính thể tích của khối trụ tròn xoay có nhiều điểm tương đồng với công thức tính thể tích của khối lăng trụ, vì cả hai đều sử dụng diện tích đáy nhân với chiều cao.
3. Các dạng bài tập về thể tích của khối trụ tròn xoay từ cơ bản đến nâng cao
Công thức tính thể tích khối trụ tròn xoay có thể được áp dụng để giải quyết nhiều dạng bài tập khác nhau. Dưới đây là một số dạng bài tập phổ biến:
3.1. Dạng 1: Tìm bán kính đáy của khối trụ tròn xoay
Phương pháp giải
- Nếu đề bài cho đường kính mặt đáy tròn, chỉ cần chia 2 để có bán kính.
- Nếu đề cho chu vi mặt đáy, sử dụng công thức \(\text{Chu vi} = 2\pi r\) để tính bán kính.
Ví dụ: Cho khối trụ tròn xoay có thể tích bằng \( \pi a^{3} \), chiều cao là \( h = 2a \). Tìm bán kính đáy \( r \) của khối trụ đó.
Lời giải:
Áp dụng công thức tính thể tích:
\[ V = \pi r^{2} h \]
Với \( V = \pi a^{3} \) và \( h = 2a \):
\[ \pi a^{3} = \pi r^{2} (2a) \]
Suy ra:
\[ r^{2} = \frac{a^{3}}{2a} = \frac{a^{2}}{2} \]
\[ r = \frac{a \sqrt{2}}{2} \]
Vậy bán kính đáy của khối trụ tròn xoay đó là: \( \frac{a \sqrt{2}}{2} \).
3.2. Dạng 2: Tìm diện tích đáy tròn
Để tìm diện tích đáy tròn của khối trụ, ta sử dụng công thức tính diện tích hình tròn:
\[ S = \pi r^{2} \]
Ví dụ: Cho khối trụ tròn xoay có diện tích toàn phần gấp 2 lần diện tích xung quanh và có bán kính đáy bằng 6cm. Tính thể tích khối trụ đó.
Giải:
Diện tích toàn phần của khối trụ là:
\[ S_{TP} = 2S_{xq} \]
Biết rằng:
\[ S_{xq} = 2\pi rh \]
Ta có:
\[ 2 (2\pi rh) = 2\pi r (r + h) \]
Giải ra ta tìm được chiều cao \( h = 6 \) cm.
Sau đó, thể tích được tính bằng:
\[ V = \pi r^{2} h = \pi (6^{2}) (6) = 678.6 \, cm^{3} \]
3.3. Dạng 3: Tìm chiều cao của hình trụ
Trong một số bài tập, nếu biết độ dài đường chéo đến hình tròn đáy, ta có thể sử dụng định lý Pytago để tính chiều cao của hình trụ.
Ví dụ: Cho khối trụ có thể tích bằng \( 12\pi \), chu vi đáy là \( 2\pi \). Tính thể tích của khối trụ đó.
Lời giải:
Bán kính đáy của khối trụ là:
\[ r = \frac{2\pi}{2\pi} = 1 \]
Chiều cao của khối trụ là:
\[ h = \frac{V}{\pi r^{2}} = \frac{12\pi}{\pi \cdot 1^{2}} = 12 \]
Vậy chiều cao của khối trụ là 12.
4. Một số bài tập tính thể tích khối trụ tròn xoay (kèm lời giải chi tiết)
Bài 1:
Cho hình trụ tròn xoay có hai đáy là hai đường tròn có tâm O và O', A và B lần lượt nằm trên hai đường tròn đó. Biết rằng AB tạo với trục OO' góc \( \alpha \) và AB = a. Tính thể tích khối trụ, biết khoảng cách giữa AB và OO' bằng d.
Lời giải:
- Chiều cao của khối trụ là \( h = OO' = a \cos \alpha \).
- Bán kính đáy là:
\[ r = \sqrt{IC^{2} + O'I^{2}} = \sqrt{\frac{1}{4}a^{2}\sin^{2}\alpha + d^{2}} \]
Vậy thể tích của khối trụ là:
\[ V = \pi r^{2}h = \pi \left( \frac{1}{4}a^{2}\sin^{2}\alpha + d^{2} \right) a \cos \alpha \]
Bài 2:
Cho khối trụ tròn xoay có đáy là hình tròn ngoại tiếp của tam giác đều cạnh a. Biết chiều cao khối trụ là 3a. Tính thể tích khối trụ tròn xoay đó.
Lời giải:
- Bán kính đáy của khối trụ là:
\[ r = \frac{a\sqrt{3}}{3} \]
- Thể tích của khối trụ là:
\[ V = \pi r^{2} h = \pi \left( \frac{a\sqrt{3}}{3} \right)^{2} (3a) = \pi a^{3} \]
Bài 3:
Cho khối trụ có chu vi đáy bằng 20cm, diện tích xung quanh khối trụ bằng 14cm². Tính thể tích và chiều cao của khối trụ.
Lời giải:
\[ 2\pi r = 20 \Rightarrow r = \frac{20}{2\pi} \approx 3.18 \, cm \]
- Chiều cao của khối trụ là:
\[ S_{xq} = 2\pi rh = 20h = 14 \Rightarrow h = \frac{14}{20} = 0.7 \, cm \]
\[ V = \pi r^{2} h = \pi (3.18)^{2} (0.7) \approx 21.99 \, cm^{3} \]
Ngoài ra, các em có thể tham khảo thêm những cách giải nhanh và thú vị hơn trong video bài giảng về thể tích khối tròn xoay.
Kết luận
Trên đây là toàn bộ lý thuyết và bài tập cơ bản về khối trụ tròn xoay cùng với công thức tính thể tích. Hy vọng qua bài viết này, các bạn đã nắm rõ được khái niệm, công thức và cách thức giải các bài tập liên quan đến khối trụ tròn xoay. Đừng quên truy cập các trang học trực tuyến và đăng ký để có thêm nhiều kiến thức bổ ích về toán học!
Tham khảo thêm:
- Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết.
- Xem thêm các công thức tính thể tích khối cầu, khối chóp và các hình không gian khác để củng cố kiến thức nhé!


























