Tìm hiểu về Bán kính của đường tròn trong hình học

Giới thiệu về hình tròn và các khái niệm liên quan

Hình tròn là một trong những hình dạng cơ bản và phổ biến trong toán học và đời sống hàng ngày. Với những đặc điểm độc đáo, hình tròn không chỉ xuất hiện trong các bài toán hình học mà còn trong nhiều lĩnh vực khác nhau như vật lý, kỹ thuật, và nghệ thuật. Trong bài viết này, chúng ta sẽ tìm hiểu về một trong những yếu tố quan trọng nhất của hình tròn, đó là khoảng cách từ tâm hình tròn đến bất kỳ điểm nào trên chu vi của nó.

Các khái niệm cơ bản về hình tròn

Tâm của hình tròn

Tâm của hình tròn là điểm nằm chính giữa của hình tròn. Từ tâm, chúng ta có thể xác định được các khoảng cách đến chu vi của hình tròn. Tâm thường được ký hiệu bằng chữ "O".

Đường kính

Đường kính là đoạn thẳng dài nhất của hình tròn, nối hai điểm trên chu vi và đi qua tâm. Đường kính là một trong những yếu tố quan trọng để tính toán nhiều thông số liên quan đến hình tròn.

Bán kính

Khoảng cách từ tâm đến chu vi, hay còn gọi là bán kính, là một trong những yếu tố chính giúp xác định kích thước của hình tròn. Trong hình học, bán kính thường được ký hiệu bằng chữ "r". Để tính bán kính, bạn có thể sử dụng công thức đơn giản: bán kính bằng một nửa đường kính.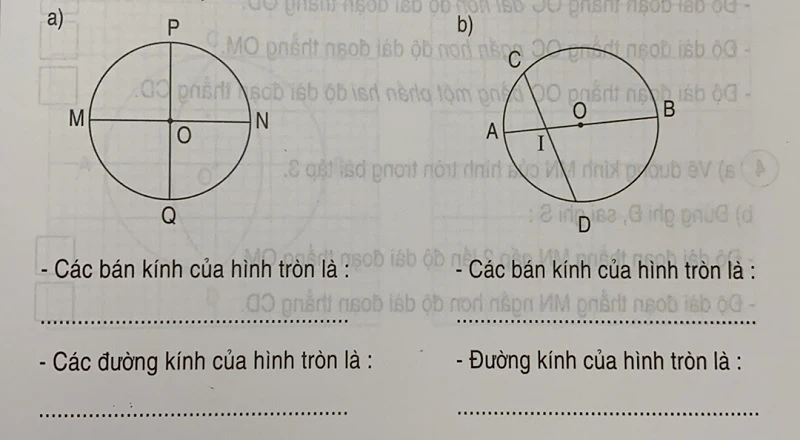

Cách tính bán kính của hình tròn

Để tính bán kính, có một số công thức mà bạn có thể áp dụng. Dưới đây là các cách tính phổ biến nhất:

Tính bán kính từ chu vi

Nếu bạn biết chu vi của hình tròn, bạn có thể tính bán kính dễ dàng bằng công thức sau: \[ r = \frac{C}{2\pi} \] Trong đó:

• \( r \) là bán kính
• \( C \) là chu vi
• \( \pi \) là hằng số Pi (khoảng 3.14)

Ví dụ, nếu chu vi của hình tròn là 31.4 cm, bạn có thể tính bán kính như sau: \[ r = \frac{31.4}{2 \times 3.14} = 5 \text{ cm} \]

Tính bán kính từ diện tích

Nếu bạn biết diện tích của hình tròn, bạn cũng có thể tính bán kính bằng cách sử dụng công thức: \[ r = \sqrt{\frac{S}{\pi}} \] Trong đó, \( S \) là diện tích của hình tròn. Ví dụ, nếu diện tích của hình tròn là 78.5 cm²: \[ r = \sqrt{\frac{78.5}{3.14}} \approx 5 \text{ cm} \]

Một số ứng dụng của bán kính trong thực tế

Bán kính không chỉ là một khái niệm toán học trừu tượng, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống hàng ngày cũng như trong các lĩnh vực nghiên cứu. Dưới đây là một số ứng dụng điển hình:

Trong xây dựng

Trong ngành xây dựng, bán kính thường được sử dụng để thiết kế các cấu trúc hình tròn như cầu, mái vòm và các công trình kiến trúc khác. Việc xác định chính xác bán kính giúp các kỹ sư tính toán các thông số như tải trọng và độ ổn định của công trình.

Trong vật lý

Đặc biệt trong vật lý, bán kính có thể ảnh hưởng đến các hiện tượng như lực hấp dẫn và lực ly tâm. Ví dụ, trong cơ học, bán kính sẽ ảnh hưởng đến tốc độ quay của một đối tượng xung quanh một điểm.

Trong công nghệ

Trong lĩnh vực công nghệ, bán kính cũng rất quan trọng trong việc thiết kế các linh kiện điện tử dạng tròn, như đĩa cứng hoặc các thành phần trong các thiết bị gia dụng.

Kết luận

Khoảng cách từ tâm đến chu vi của hình tròn là một yếu tố cơ bản nhưng cực kỳ quan trọng trong toán học và nhiều lĩnh vực khác. Việc hiểu rõ và áp dụng đúng các công thức liên quan đến bán kính không chỉ giúp bạn giải quyết các bài toán hình học mà còn có thể áp dụng trong thực tế. Hãy luôn ghi nhớ rằng, bán kính không chỉ đơn giản là một số đo, mà còn là nền tảng cho nhiều khái niệm và ứng dụng quan trọng trong cuộc sống. Hy vọng qua bài viết này, bạn đã có cái nhìn sâu sắc hơn về khoảng cách từ tâm đến chu vi của hình tròn và những ứng dụng thực tiễn của nó trong đời sống hàng ngày.