Công thức tính thể tích hình hộp chữ nhật đơn giản

Trong bài viết này, Viện đào tạo Vinacontrol sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về công thức tính thể tích hình hộp chữ nhật. Bài viết sẽ đi từ lý thuyết đến các bài tập thực hành để bạn có thể hiểu và áp dụng một cách dễ dàng.

1. Công Thức Tính Thể Tích Hình Hộp Chữ Nhật

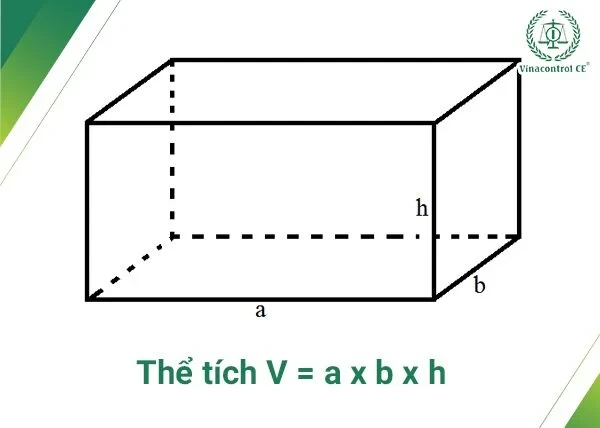
Để tính thể tích của một hình hộp chữ nhật, bạn chỉ cần áp dụng công thức đơn giản: Công thức: \[ V = a \times b \times h \] Trong đó:

• \( V \): Thể tích hình hộp chữ nhật
• \( a \): Chiều dài
• \( b \): Chiều rộng
• \( h \): Chiều cao

Ví dụ Cụ Thể

Giả sử bạn có một hình hộp chữ nhật với chiều dài là 5cm, chiều rộng là 4cm và chiều cao là 2cm. Thể tích của hình hộp này sẽ được tính như sau: \[ V = 5 \times 4 \times 2 = 40 \, cm^3 \] Xem thêm:

2. Các Dạng Bài Tập Liên Quan Đến Công Thức Tính Thể Tích Hình Hộp Chữ Nhật

2.1. Tính Thể Tích Của Một Hộp Chữ Nhất Đã Biết Kích Thước

Ví dụ: Tính thể tích của một hộp chữ nhật có chiều dài 4cm, chiều rộng 3cm và chiều cao 2cm. Giải: \[ V = a \times b \times h = 4 \times 3 \times 2 = 24 \, cm^3 \]

2.2. Tính Một Trong Ba Kích Thước Khi Biết Thể Tích và Hai Kích Thước Khác

Ví dụ: Tính chiều rộng của một hộp chữ nhật có thể tích 240cm³, chiều dài 4cm và chiều cao 5cm. Giải: \[ V = a \times b \times h \Rightarrow 240 = 4 \times b \times 5 \Rightarrow b = 12 \, cm \]

2.3. Tìm Chiều Cao Khi Đã Biết Thể Tích và Hai Kích Thước Khác

Ví dụ: Tìm chiều cao của một hộp chữ nhật có thể tích 420cm³, chiều dài 14cm và chiều rộng 3cm. Giải: \[ V = a \times b \times h \Rightarrow 420 = 14 \times 3 \times h \Rightarrow h = 10 \, cm \]

2.4. Tính Thể Tích Hộp Chữ Nhật Bị Cắt Bỏ Một Phần

Ví dụ: Tính thể tích của một hộp chữ nhật có chiều dài 12cm, chiều rộng 6cm và chiều cao 3cm nếu một phần của hộp bị cắt bỏ. Giải: \[ V = (12 \times 6 \times 3) - (4 \times 3 \times 3) = 216 - 36 = 180 \, cm^3 \]

2.5. Tính Thể Tích Hộp Chữ Nhật Có Lỗ Hình Tròn

Ví dụ: Tính thể tích của một hộp chữ nhật có chiều dài 10cm, chiều rộng 8cm và chiều cao 6cm nếu một lỗ hình tròn bán kính 2cm được đục ra khỏi một mặt phẳng của nó. Giải: \[ V = (10 \times 8 \times 6) - (\pi \times 2^2 \times 6) \approx 480 - 25.12 \approx 454.88 \, cm^3 \]

2.6. Tính Thể Tích Hộp Chữ Nhật Không Đều

Ví dụ: Tính thể tích của một hộp chữ nhật không đều với chiều dài 10cm, chiều rộng 5cm và chiều cao 4cm, trong đó mặt phẳng dưới cùng là một hình tam giác đều với cạnh 6cm. Giải: \[ V = (10 \times 5 \times 4) + \left(\frac{1}{2} \times 6 \times 4\right) = 200 + 12 = 212 \, cm^3 \] Xem thêm:

3. Các Bài Tập Tự Luyện Tại Nhà

Để rèn luyện thêm về kỹ năng tính thể tích hình hộp chữ nhật, dưới đây là một số bài tập mà bạn có thể thực hiện:

Câu Hỏi Tự Luyện

• Một vòi nước mỗi giờ chảy được 500 lít nước. Hỏi vòi nước chảy đầy bể nước dạng hình hộp chữ nhật có chiều dài 5m, chiều rộng 1,5m và chiều cao 1,6m sẽ mất bao lâu?
• Một hình lập phương có thể tích là 25000cm³. Hỏi diện tích xung quanh và diện tích toàn phần của hình lập phương đó bằng bao nhiêu?
• Người ta xây một bể bơi dạng hình lập phương cạnh 16m. Hỏi để đổ đầy bể nước đó thì cần bao nhiêu lít nước?
• Một bể nước hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể là 0,8m.

- a) Tính chiều rộng của bể nước. - b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?

• Cho tấm bìa hình hộp chữ nhật có chiều dài 15cm, chiều rộng 9cm, chiều cao 12cm. Tính thể tích của tấm bìa hình hộp chữ nhật đó?
• Một bể nước hình hộp chữ nhật có các kích thước trong bể là chiều dài 3m; chiều rộng kém chiều dài 1,8m; chiều cao 1,5m. Hỏi bể đó chứa được nhiều nhất bao nhiêu lít nước? (1 lít = 1dm³)
• Tính thể tích hình hộp chữ nhật không nắp biết chiều dài 75 cm, chiều rộng 40 cm và chiều cao 35 cm.
• Tính thể tích của một hình hộp chữ nhật có diện tích xung quanh bằng 448 cm², chiều cao 8 cm, chiều dài hơn chiều rộng 4 cm.
• Tính thể tích hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c:

- a) a = 7 cm; b = 5 cm; c = 12cm - b) a = 3 m; b = 2 m; c = 1 m

• Một bể cá dạng hình hộp chữ nhật có chiều dài 90cm, chiều rộng là 50cm và chiều cao 75cm. Mực nước ban đầu trong bể cao 45cm. Người ta cho vào bể một hòn đá có thể tích 18dm³. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng-ti-mét?

Trên đây là toàn bộ nội dung về công thức tính thể tích hình hộp chữ nhật. Hy vọng rằng những kiến thức mà Viện đào tạo Vinacontrol cung cấp sẽ giúp ích cho quá trình học tập của bạn. Đừng quên thực hành các bài tập tự luyện để củng cố thêm kỹ năng của mình!

Tham Khảo Các Công Thức Toán Học Khác

• Xem thêm:
• Xem thêm:
• Xem thêm:
• Xem thêm:

Mọi thắc mắc hay cần thêm thông tin, bạn hãy liên hệ với chúng tôi để được giải đáp kịp thời!