Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng

Hình Chóp Tứ Giác Đều: Một Khái Niệm Quan Trọng Trong Hình Học Không Gian Hình chóp tứ giác đều là một khái niệm không thể thiếu trong hình học không gian. Nó không chỉ xuất hiện nhiều trong sách giáo khoa mà còn thường xuyên có mặt trong các bài kiểm tra và kỳ thi. Để giúp bạn hiểu rõ hơn về hình chóp tứ giác đều, Mytour xin giới thiệu nội dung chi tiết dưới đây, từ định nghĩa đến các tính chất và ứng dụng của nó.

1. Hình Chóp Tứ Giác Đều Là Gì?

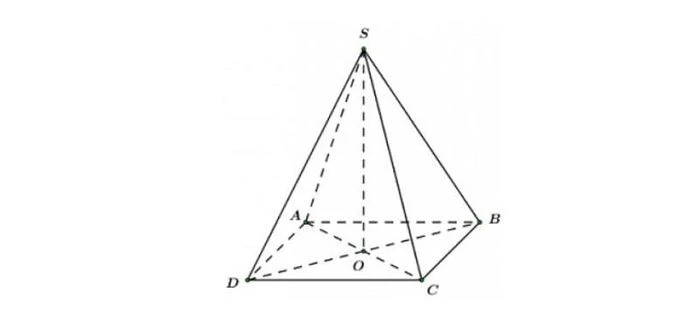
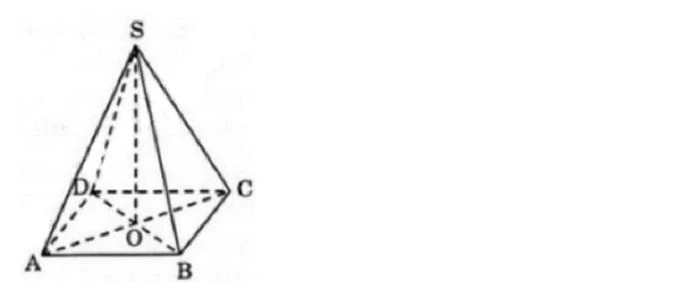
Hình chóp tứ giác đều là một khối hình học ba chiều, cấu tạo từ một tứ giác làm đáy và một điểm nằm bên ngoài mặt phẳng của tứ giác đó. Đỉnh hình chóp nằm trên một trục thẳng đứng, vuông góc với đáy. Cách đơn giản để hình dung hình chóp tứ giác là hình dạng của một chiếc kén, với đỉnh là điểm cao nhất và đáy là một hình vuông.

1.1. Định Nghĩa và Các Tính Chất Cơ Bản

Định nghĩa hình chóp tứ giác đều được mô tả như sau:

• Đáy: Là một hình vuông, tức là tứ giác đều với bốn cạnh bằng nhau.
• Đỉnh: Là một điểm nằm trên trục vuông góc với mặt phẳng của đáy.
• Cạnh bên: Các đoạn thẳng nối từ đỉnh đến các đỉnh của tứ giác đáy.

Hình chóp tứ giác đều có những tính chất nổi bật như:

• Các cạnh bên đều có độ dài bằng nhau.
• Các mặt bên đều là các tam giác cân.
• Đường cao của hình chóp đi qua trung điểm của các cạnh đáy.

2. Hình Chóp Tứ Giác Đều Có Bao Nhiêu Mặt Phẳng Đối Xứng?

Để trả lời câu hỏi "Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?", chúng ta cần tìm hiểu về mặt phẳng đối xứng trong hình học.

2.1. Định Nghĩa Mặt Phẳng Đối Xứng

Một mặt phẳng (P) được gọi là mặt phẳng đối xứng của hình (H) nếu phép đối xứng qua (P) làm hình (H) trùng với chính nó. Trong trường hợp của hình chóp tứ giác đều, có tổng cộng 4 mặt phẳng đối xứng. Cụ thể:

• Mặt phẳng (SAC): Chia đều hình chóp thành hai nửa giống hệt nhau thông qua đỉnh S và đường chéo AC của đáy.
• Mặt phẳng (SBD): Tương tự như vậy, mặt phẳng này đi qua đỉnh S và đường chéo BD.
• Mặt phẳng (SIK): Đi qua đỉnh S và trung điểm của đoạn thẳng nối các cạnh đáy.
• Mặt phẳng (SMN): Cũng tương tự, mặt phẳng này chia đáy thành hai phần đối xứng.

2.2. Hình Ảnh Mô Tả Mặt Phẳng Đối Xứng

Nếu bạn nhìn vào hình chóp tứ giác đều, các mặt phẳng đối xứng này sẽ giúp bạn nhận ra sự cân đối và hài hòa trong cấu trúc của hình. Các mặt phẳng này không chỉ là lý thuyết mà còn có thể được xác định qua phép đo thực tế.

3. Các Đặc Điểm Nổi Bật Của Hình Chóp Tứ Giác Đều

Khi bạn đã hiểu về mặt phẳng đối xứng, hãy cùng khám phá những đặc điểm nổi bật khác của hình chóp tứ giác đều:

• Cạnh Bên: Được cấu tạo từ các cạnh bên đều có chiều dài giống nhau, tạo nên sự đồng nhất đáng kể.
• Mặt Bên: Các mặt bên của hình chóp đều là các tam giác cân, điều này có nghĩa là các góc giữa cạnh bên và mặt đáy đều bằng nhau.
• Trọng Tâm: Trọng tâm của hình chóp tứ giác đều là điểm nơi các đường trung tuyến, đường phân giác và đường cao gặp nhau.

4. Công Thức Liên Quan Đến Hình Chóp Tứ Giác Đều

4.1. Diện Tích và Thể Tích

Để tính toán diện tích và thể tích của hình chóp tứ giác đều, bạn có thể sử dụng các công thức sau:

• Diện tích xung quanh (Sxq): Được tính bằng nửa chu vi đáy nhân với chiều cao của trung đoạn.

Công thức: \[ Sxq = p \cdot d \] (Trong đó \(p\) là nửa chu vi đáy, \(d\) là chiều cao trung đoạn)

• Diện tích toàn phần (Stp): Là tổng diện tích xung quanh và diện tích mặt đáy.

Công thức: \[ Stp = Sxq + S \] (Trong đó \(S\) là diện tích của đáy)

• Thể tích (V): Được tính bằng một phần ba diện tích đáy nhân với chiều cao.

Công thức: \[ V = \frac{1}{3} \cdot S_{ABCD} \cdot SO \] Trong đó \(S_{ABCD}\) là diện tích hình vuông đáy và \(SO\) là chiều cao từ điểm O xuống trung tâm của đáy ABCD.

5. Một Số Bài Tập Ứng Dụng

Để củng cố kiến thức, dưới đây là một số bài tập ứng dụng có liên quan đến hình chóp tứ giác đều:

Bài Tập 1:

Cho khối chóp tứ giác SABCD với tất cả các cạnh có độ dài bằng a. Chứng minh rằng khối chóp SABCD là hình chóp tứ giác đều và tính thể tích của nó. Hướng dẫn giải:

• Vẽ đường thẳng SO vuông góc với mặt đáy ABCD.
• Vì \(SA = SB = SC = SD\) nên \(OA = OB = OC = OD\).
• Kết luận: ABCD là hình vuông, từ đó tính thể tích bằng công thức đã nêu ở trên.

Bài Tập 2:

Xác định tâm và bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD, với các cạnh đều có độ dài a. Hướng dẫn giải:

• Điểm O là hình chiếu của điểm A lên mặt phẳng hình vuông ABCD, do đó, O là tâm của hình vuông ABCD.
• Các đoạn OA, OB, OC, OD, và OS đều bằng nhau, từ đó xác định bán kính của mặt cầu ngoại tiếp.

6. Tóm Tắt

Hình chóp tứ giác đều không chỉ đơn thuần là một khái niệm trong hình học mà còn là một phần quan trọng trong toán học ứng dụng, từ việc tính toán diện tích, thể tích cho đến việc khám phá các đặc tính đối xứng. Qua bài viết này, Mytour hy vọng đã cung cấp cho bạn cái nhìn tổng quan về hình chóp tứ giác đều, các mặt phẳng đối xứng và những ứng dụng thực tế của nó. Nếu bạn có bất kỳ câu hỏi nào hoặc cần thêm thông tin, đừng ngần ngại để lại câu hỏi cho chúng tôi. Cảm ơn bạn đã theo dõi bài viết này!