Khám Phá Hình Elip và Định Nghĩa Trong Toán Học

Hình elip là một trong những khái niệm cơ bản trong hình học và đại số mà học sinh lớp 10 thường gặp. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về định nghĩa, phương trình, cũng như các bài tập liên quan đến hình elip. Hy vọng rằng các kiến thức này sẽ giúp các bạn củng cố tốt hơn kiến thức Toán học của mình.

1. Định Nghĩa Hình Elip

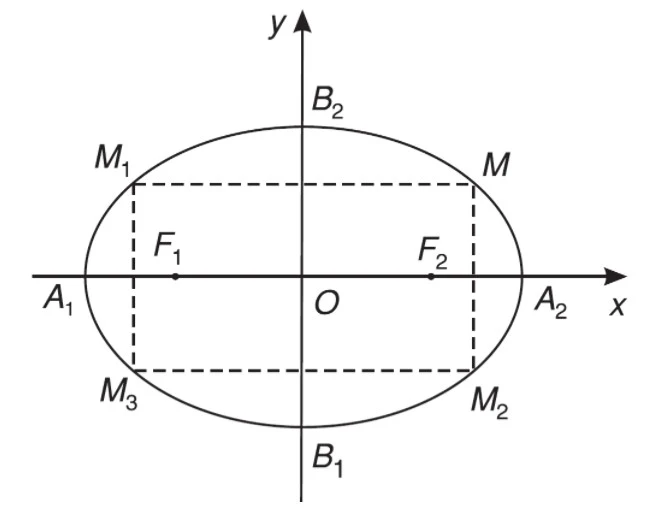
Trong mặt phẳng, hình elip được định nghĩa là tập hợp các điểm M sao cho tổng khoảng cách từ hai tiêu điểm F1 và F2 đến điểm M là không đổi. Cụ thể:

• Tiêu điểm: Hai điểm F1 và F2 được gọi là tiêu điểm.
• Tiêu cự: Khoảng cách giữa hai tiêu điểm F1 và F2 được gọi là tiêu cự, ký hiệu là 2c.
• Tổng khoảng cách: Tổng F1M + F2M = 2a, trong đó a là bán trục lớn của elip.

Hình elip có nhiều ứng dụng trong thực tế, từ vật lý đến thiên văn học. Việc hiểu rõ về hình elip sẽ giúp bạn có một cái nhìn tổng quát hơn về các đường cong trong không gian.

2. Phương Trình Chính Tắc Của Hình Elip

2.1. Phương Trình Chính Tắc

Cho elip có tiêu điểm F1, F2, và chọn hệ trục tọa độ Oxy sao cho F1(-c; 0) và F2(c; 0). Ta có phương trình chính tắc của elip như sau: $$ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 $$ Trong đó, b² = a² - c².

2.2. Ví Dụ Cụ Thể

Giả sử chúng ta có một elip với độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Ta cần xác định phương trình chính tắc của elip này.

• Độ dài trục lớn: 2a = 12 ⇒ a = 6.
• Độ dài trục bé: 2b = 6 ⇒ b = 3.

Vậy, phương trình của elip sẽ là: $$ \frac{x^{2}}{36} + \frac{y^{2}}{9} = 1 $$

3. Thành Phần Và Hình Dạng Của Hình Elip

Khi nghiên cứu về hình elip, chúng ta cần chú ý đến các thành phần và hình dạng của nó.

3.1. Các Trục Đối Xứng

Elip có các trục đối xứng qua hai trục tọa độ:

• Trục lớn: Đi qua hai đỉnh A1 và A2.
• Trục nhỏ: Đi qua hai đỉnh B1 và B2.

3.2. Tâm Đối Xứng

Tâm đối xứng của elip luôn là gốc O (0, 0).

3.3. Các Điểm Cắt Với Trục Oxy

• Khi y = 0, từ phương trình chính tắc, ta có x = ±a. Do đó, elip cắt trục Ox tại hai điểm A1(-a, 0) và A2(a, 0).
• Khi x = 0, ta có y = ±b. Do đó, elip cắt trục Oy tại hai điểm B1(0, -b) và B2(0, b).

3.4. Ví Dụ

Cho elip có phương trình: $$ \frac{x^{2}}{25} + \frac{y^{2}}{9} = 1 $$ Ta tính được:

• a² = 25 ⇒ a = 5
• b² = 9 ⇒ b = 3
• c = √(a² - b²) = √(25 - 9) = 4

Các thông số của elip này là:

• Trục lớn: A1A2 = 2a = 10
• Trục nhỏ: B1B2 = 2b = 6
• Hai tiêu điểm: F1(-4, 0), F2(4, 0)
• Bốn đỉnh: A1(-5, 0), A2(5, 0), B1(0, -3), B2(0, 3)

4. Các Dạng Bài Tập Về Hình Elip

4.1. Bài Tập 1: Tính Khoảng Cách

Cho elip (E): $$ \frac{x^{2}}{16}+\frac{y^{2}}{12}=1 $$ Điểm M nằm trên elip có hoành độ bằng 1, hãy tính các khoảng cách từ M đến hai tiêu điểm của (E). Giải:

• a² = 16 ⇒ a = 4
• b² = 12 ⇒ b = 2√3
• c² = a² - b² = 16 - 12 = 4 ⇒ c = 2

Các tiêu điểm là F1(-2, 0) và F2(2, 0). Điểm M có tọa độ (1, y):

• Tính y từ phương trình elip:

$$ \frac{1^{2}}{16} + \frac{y^{2}}{12} = 1 \Rightarrow y^{2} = 12(1 - \frac{1}{16}) = 12 \cdot \frac{15}{16} = \frac{180}{16} = \frac{45}{4} $$ Vậy y = ±(3√5/2). Khoảng cách từ M đến hai tiêu điểm được tính như sau:

• Khoảng cách tới F1: MF1 = a + exM = 4 + 0.5 = 4.5
• Khoảng cách tới F2: MF2 = a - exM = 4 - 0.5 = 3.5

4.2. Bài Tập 2: Viết Phương Trình Chính Tắc

Trong mặt phẳng tọa độ, viết phương trình chính tắc của elip (E) có tâm sai bằng √3/3 và độ dài đường chéo hình chữ nhật cơ sở bằng 2√5. Giải:

• Gọi phương trình (E) có dạng:

$$ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 $$ với a > b > 0. Từ tâm sai: $$ e = \frac{c}{a} = \frac{\sqrt{3}}{3} \Rightarrow c² = \frac{a²}{3} $$ Đường chéo hình chữ nhật: $$ \sqrt{(2a)^{2} + (2b)^{2}} = 2\sqrt{5} \Rightarrow a^{2} + b^{2} = 5 $$ Từ mối quan hệ: $$ a^{2} = b^{2} + c^{2} $$ Sẽ giải ra được các giá trị của a và b.

5. Kết Luận

Từ những kiến thức trong bài viết này, hy vọng các bạn đã có thể hình dung rõ hơn về hình elip, từ định nghĩa, phương trình đến cách giải các bài tập liên quan. Hình elip không chỉ là một khái niệm trong sách vở mà còn có nhiều ứng dụng trong thực tế. Để tiếp tục học hỏi và rèn luyện, các bạn có thể tham khảo thêm tài liệu và các nguồn học trực tuyến. Nếu bạn cảm thấy bài viết hữu ích, hãy chia sẻ cho bạn bè để cùng nhau tìm hiểu thêm về các khái niệm thú vị trong Toán học nhé!