Z là tập hợp số gì? Các dạng bài tập về số nguyên Z

Tập Hợp Z Là Gì? Cùng Khám Phá Tập Hợp Số Nguyên Đầy Thú Vị! Toán học là một lĩnh vực không chỉ khô khan mà còn đầy màu sắc với các ký hiệu và tập hợp số khác nhau. Một trong những ký hiệu quan trọng nhất mà bạn sẽ gặp trong hành trình khám phá toán học đó chính là ký hiệu Z. Vậy tập hợp Z là gì? Chúng ta hãy cùng M5s News đi sâu vào tìm hiểu về tập hợp số nguyên này, những đặc điểm nổi bật, ví dụ minh họa và các bài tập liên quan nhé!

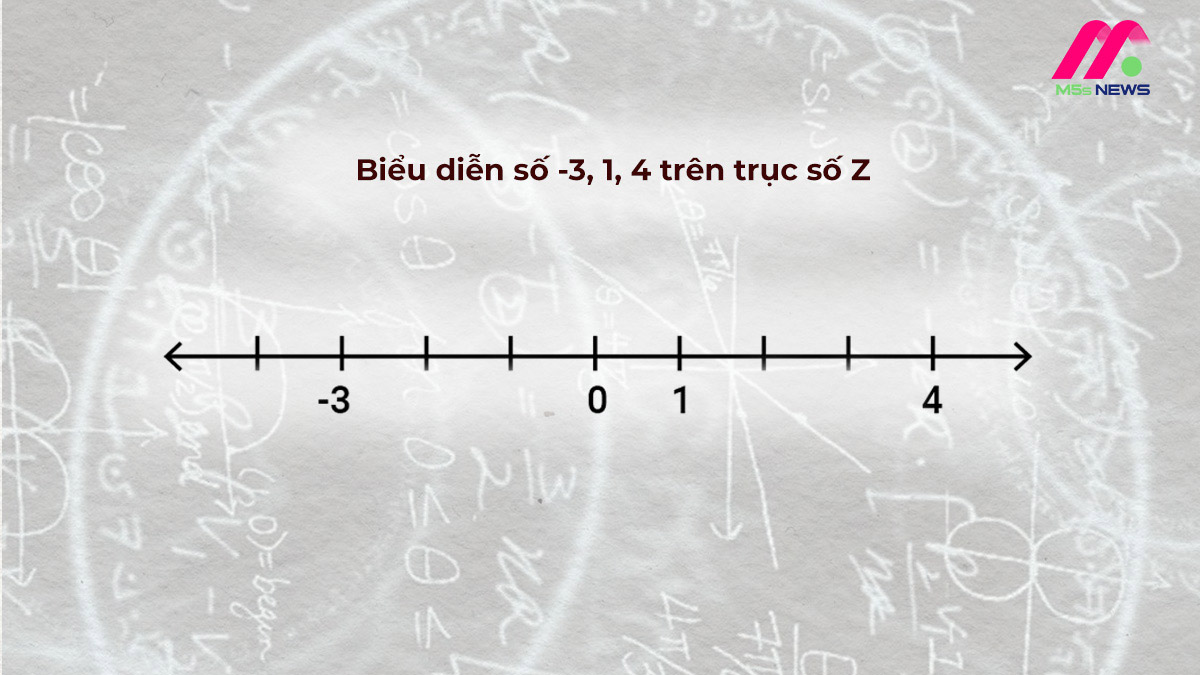
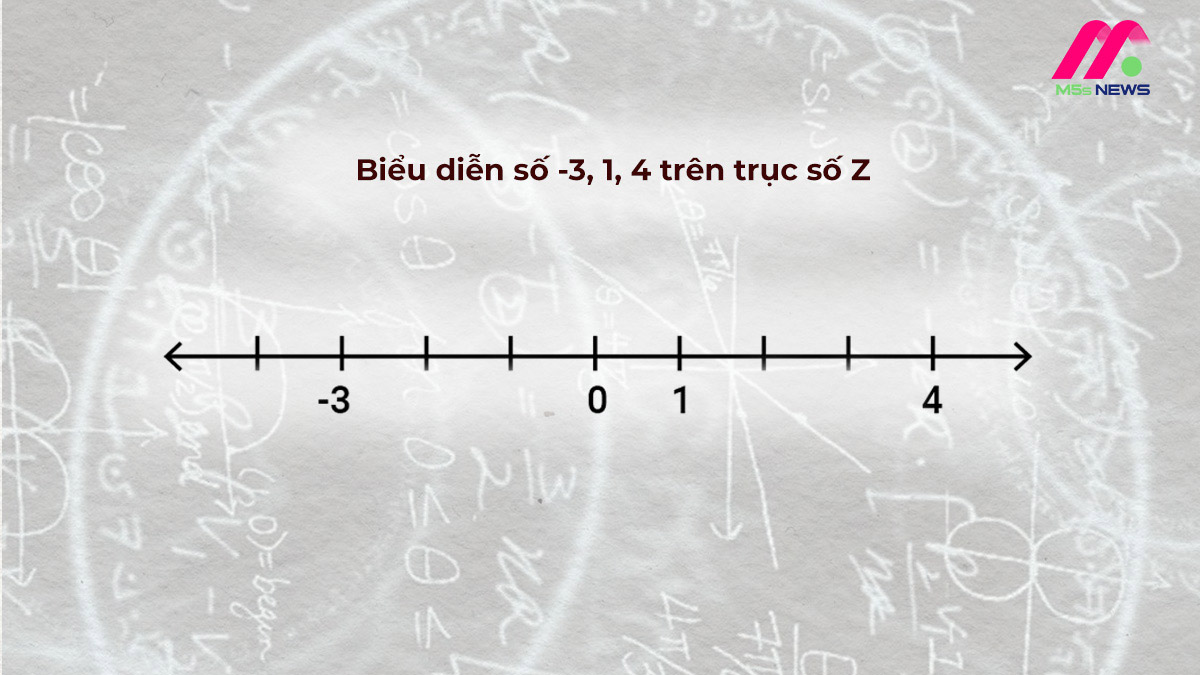
1. Tập Hợp Z Là Gì?

Định Nghĩa Tập Hợp Z Tập hợp Z được định nghĩa là tập hợp các số nguyên, bao gồm cả số nguyên dương, số nguyên âm và số 0. Ký hiệu này được lấy từ từ tiếng Đức "Zahlen", có nghĩa là "các số". Ví Dụ Cụ Thể Một cách hiểu đơn giản là tập hợp Z bao gồm các số như sau:

• Số nguyên âm: -3, -2, -1
• Số 0: 0
• Số nguyên dương: 1, 2, 3

Như vậy, tập hợp Z có thể được biểu diễn bằng: \[ Z = \{..., -3, -2, -1, 0, 1, 2, 3, ...\} \]

2. Ký Hiệu và Phân Nhóm Của Tập Hợp Z

Tập hợp Z không chỉ đơn thuần là một tập hợp mà còn được chia thành các tập con khác nhau:

• Tập hợp Z+: Là tập hợp các số nguyên dương.

- Biểu diễn: \( Z+ = \{1, 2, 3, 4, ...\} \)

• Tập hợp Z-: Là tập hợp các số nguyên âm.

- Biểu diễn: \( Z- = \{-1, -2, -3, -4, ...\} \)

• Tập hợp Z*: Là tập hợp các số nguyên trừ 0.

- Biểu diễn: \( Z* = {..., -2, -1, 1, 2, ...} \)

• Tập hợp Zn: Là tập hợp các lớp tương đương của số nguyên theo modulo n.

3. Đặc Điểm Của Số Nguyên

Số nguyên là những con số không có phần thập phân hoặc phân số. Chúng bao gồm:

• Số tự nhiên dương: 1, 2, 3, ...
• Số tự nhiên âm: -1, -2, -3, ...
• Số 0

3.1 Tính Chất Của Số Nguyên

Tập hợp số nguyên Z có một số tính chất nổi bật:

• Tổng và hiệu của hai số nguyên luôn là số nguyên.
• Tích của hai số nguyên cũng là một số nguyên.
• Thương của hai số nguyên chưa chắc là số nguyên.

3.2 Ứng Dụng Trong Thực Tế

Số nguyên được ứng dụng rộng rãi trong đời sống hàng ngày, từ việc đếm số lượng, tính toán cho đến sử dụng trong các lĩnh vực khoa học, kinh tế và vật lý. Tuy nhiên, trong những trường hợp cần độ chính xác cao, số nguyên có thể không phải là lựa chọn tốt nhất.

4. So Sánh Hai Số Nguyên

So sánh hai số nguyên là một kỹ năng quan trọng trong toán học. Một vài quy tắc cơ bản:

• Nếu hai số nguyên khác dấu, số âm luôn nhỏ hơn số dương.
• Nếu hai số nguyên cùng dấu, bạn chỉ cần so sánh tuyệt đối của chúng.

Ví Dụ Minh Họa:

• So sánh -20 và -30: Vì 20 < 30, nên -20 > -30.
• So sánh 1567 và -129: 1567 > -129.

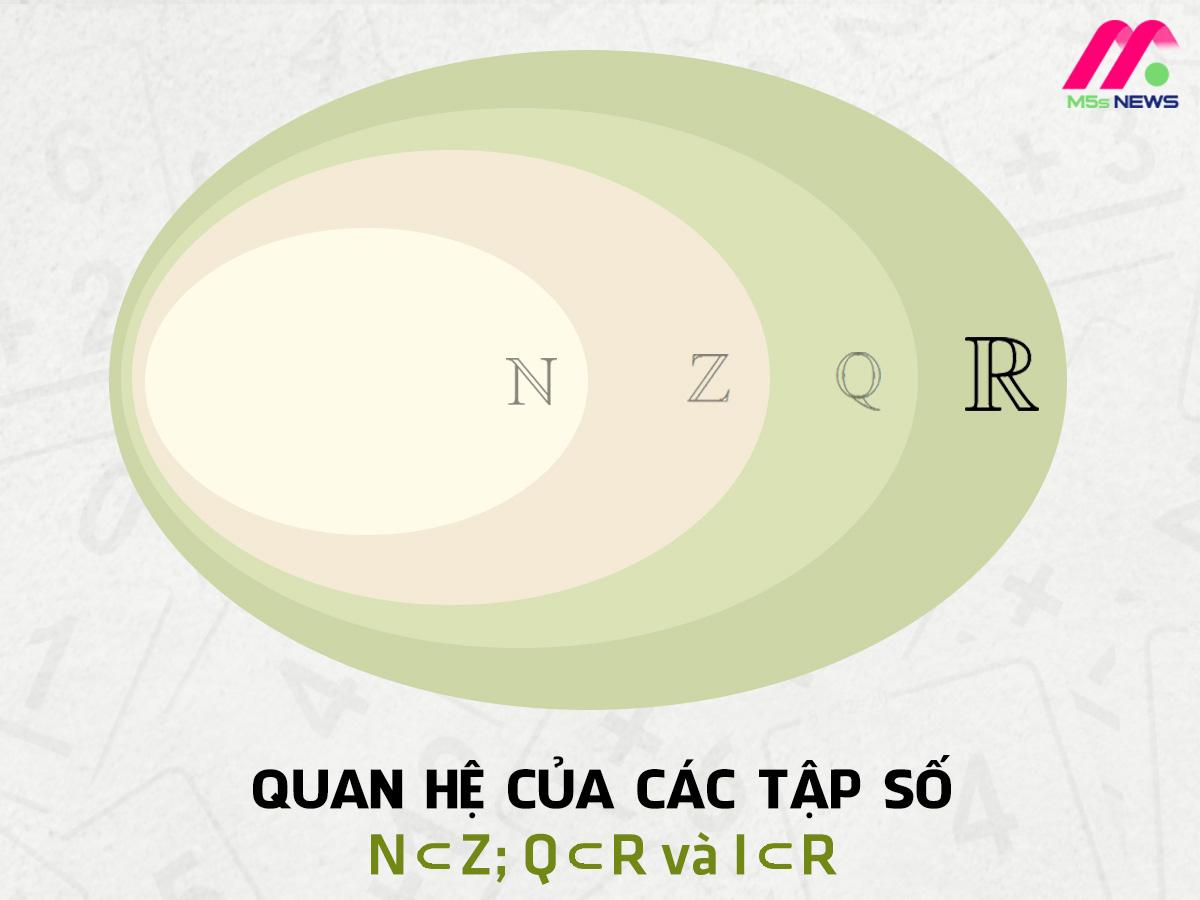
5. Quan Hệ Giữa Tập Hợp Z Với Các Tập Hợp Khác

Tập hợp Z có vị trí quan trọng trong hệ thống các tập hợp số. Quan hệ giữa các tập hợp này có thể được biểu diễn như sau: \[ N \subset Z \subset Q \subset R \]

• Tập hợp N: Các số nguyên dương.
• Tập hợp Q: Các số hữu tỉ.
• Tập hợp R: Các số thực.

6. Bài Tập Về Tập Hợp Số Nguyên Z

Để hiểu sâu hơn về tập hợp Z, chúng ta hãy giải quyết một số bài tập thú vị:

6.1 Dạng 1: Tính Giá Trị

Bài Tập:

• (-60) + 70 + 20
• (-15) + 45 - (-65)

Lời Giải:

• Bài 1: Đáp số: 30
• Bài 2: Đáp số: 95

6.2 Dạng 2: Biểu Diễn Các Điểm Trên Trục Số

Bài Tập: Vẽ các điểm trên trục số cho các số -3, 1, 4.

6.3 Dạng 3: Tìm Giá Trị x

Bài Tập:

• -1 < x < 4
• 3 < x < 10

Lời Giải:

• Bài 1: x = {0, 1, 2, 3}
• Bài 2: x = {4, 5, 6, 7, 8, 9}

7. Kết Luận

Tập hợp Z đóng vai trò rất quan trọng trong toán học, từ việc hiểu các số nguyên đến áp dụng trong thực tế. Hy vọng qua bài viết này, M5s News đã giúp bạn hiểu rõ hơn về khái niệm "tập hợp Z là gì" cũng như những bài tập liên quan đến số nguyên. Nếu bạn có bất kỳ câu hỏi nào hoặc muốn tìm hiểu thêm về các tập hợp số khác, hãy để lại bình luận bên dưới. Chúc bạn học tập tốt và khám phá thêm nhiều điều thú vị trong toán học!